| |
|
| 知识库 -> 两性话题 -> 初中数学中的平面几何没学好对高中数学的学习有影响吗? -> 正文阅读 |
|
|
[两性话题]初中数学中的平面几何没学好对高中数学的学习有影响吗? |
| [收藏本文] 【下载本文】 |
|
本人初三,平面几何方面掌握的不是很好,基本性质都知道,像什么勾股定理,锐角三角函数等等都懂,只是在应用方面想不到用不上,可能是刷题太少了吧。但是在坐标… |
|
谢邀 笔者认为:初中平几与高中立几靠的都是画图,然后想象这到底是个什么鬼 所以笔者认为图感贯穿了几何,如果没学好平几,初步立几确实会困难一点,不过到了高考那会,暴力建系才是主流(狗头) 至于在坐标系里面超好的这一点,高中会派上用场的,题主加油鸭 |

|
|
|
|
应该没有吧 在下初中就不会几何…到了高中完全没什么大问题… 高考数学147,错的是导数第二问看错定义域和值域… 除非您要搞什么进阶的数学…高考数学范围内并不需要用什么平面几何的… |
|
emmm其实还好…高中最难的又不是立几,大部分立几都是能暴力建系做出来的,不过做题速度可能比平几好的人慢很多。 平几还是超有用的,虽然高中没有直接考察平几的题,但有很多题可能用几何方法要简单的多…总之不必太过担忧但也不能松懈 |
|
负责任地告诉你是可以学好的。 高中数学不只有几何一类,而且高考考的是你综合的数学能力,你几何做得好不代表你一张卷子整体做得好,同理几何差也不意味着整体就差,我们应该学会算总账。我自己在初中时同样是几何很不好,分类啊还啥的都整不明白,但是高中时期我的数学是我的优势。 首先我们等搞清楚高中数学的特性,最最重要的是它是一门吃时间的科目,不像文科你可以用碎片化的时间去积累、背诵。它需要整块的时间。其次刷题是一定有效的。但你得分专题突破,做完一个专题之后会感觉非常有成就感。而成就感呢对你学好一样东西至关重要。切忌东一榔头西一棒子。最后呢,错题集一定一定要有。可怕的不是你题目不会不得分,而是你在同一个地方跌倒两次甚至更多次。做错题集形式不重要,你可以把做错的实体整合在一起,直接在旁边订正;也可以找一个活页本,正儿八经地做。关键是你得反复看反复做,错题本存在的意义是让你错题再练,不然的话,整得再漂亮,你也只是停留在感动自己这一层面。 你如果因为初中几何学得差而对高中数学产生畏惧。duck不必,必修一必修四都与几何无瓜,你将有很长一段时期见不着几何。好好把基础打牢,数学大佬就是你啊。 希望我的回答给你帮助,同时祝你学业进步。 |
|
没一点影响,高中及以后代数会是绝对主力,碰到的几何都可以用代数做,不用担心。几何基本上就只剩代几综合了。 |
|
高中大题的平面几何很多都是求三角函数的,或者是圆之类的,画个图没啥大不了,高中那是立体几何,可以建系,但是那样就麻烦,可以用三角函数求的立体几何就不会选择建系了=、= 有的立体几何难得里完全不知道坐标该画哪里,在得到证明前你可能还看不出那是个直角,而且你画了座标上去还觉得无从下手,为啥呢,你怀疑自己画的是不是坐标,像锐角的倾斜直角限制你的想象 |
|
你会发现立体几何你根本想象不出 |
|
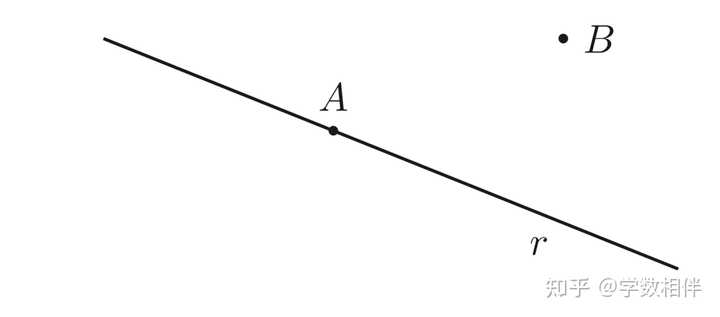
平面几何是立体几何的基础,欧氏几何就是从那几个公设推导出来的,也体现了数学不难,只要您一步步来,一切都那么自然。 第一章: 欧氏几何简介(introduction) 假设读者对点、线、面有一定的了解,我们把这些概念作为原始概念,不给正式定义。并假设直线都是由点集组成的(至少包含两个点)。 1.1 基本概念1. 点线圆 点(point): 用大写字母表示,例如 A,B,C,D,\cdots 。 直线(lines): 用小写字母表示,例如 r,s,t,\cdots 。 公理: 后续内容中,如果没有给出证明的陈述我们权当公理对待。 点和直线关系: 给定一个点 P 和一条直线 r ,则只有两种可能性 P\in r\ \lor P\not\in r 。 |
|
|
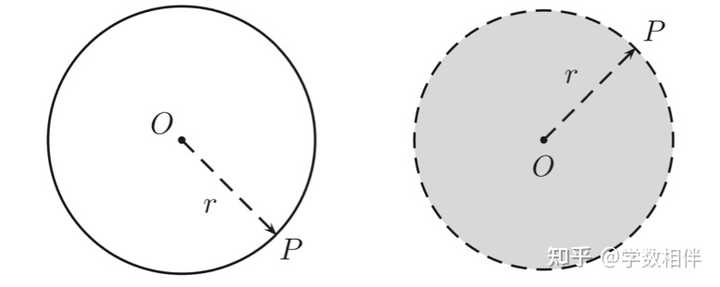
A在直线r上,B不在直线r上 公理1: 两点确定一条直线。比如 r = \overleftrightarrow{AB} , 其中 A,B 为两个不同的点,直线 r 是经过这两个点的唯一直线。 射线(half-line): 直线上任意一个点将直线分成两个半直线,也称为射线,比如记作 \overrightarrow{AB} 。 线段(line segment): 直线 r 上两个不同点 A,B 之间的部分称为线段,记作 \overline{AB} 。 注意上面关于直线、射线、线段的表示方法,分别是用双向箭头、单向箭头和无向上划线。 欧氏平面中两点之间的距离: d(A,B) = \overline{AB} 。 圆: 以点O为中心,半径 0">r>0 的圆是平面内与点O距离为r的所有点的集合,即 \overline{OP} = r 的点集。 一个圆的补集分为两部分区域,有限区域和无限区域。其中有限区域称为圆的内部(interior);无限区域称为圆的外部(exterior)。 圆的内部: \overline{OP} > r ;圆盘(disk): \overline{OP} \leq r 。 |
|
|
圆的内部及外部 |
|
|
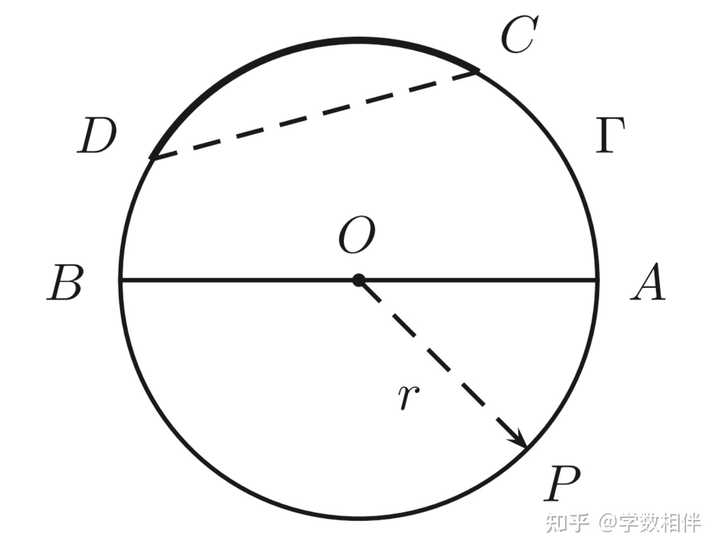
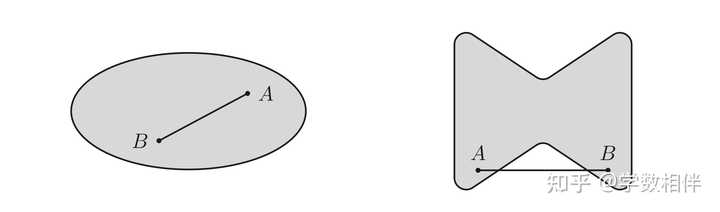
给定上述的一个圆 \Gamma(O, r) : 半径(radius): 连接圆心O和圆上一点的线段称为半径。弦(chord): 连接圆上两点的线段称为弦。直径(diameter): 过圆心的弦称为直径。半圆(semicircles): 每条直径将圆分为两个半圆。弧(arcs): 圆 \Gamma 上两点为起点和终点连通它们之间的所有点组成的曲线称为圆弧,记作 \overset{\LARGE{\frown}}{AB} 。圆上任意两点将圆分为两段弧,其中较小的弧称为minor arc(劣弧), 较大的弧称为major arc(优弧)。为了更好的区别优弧和劣弧,可以选择它们之间的第三个点来表示 \overset{\LARGE{\frown}}{ACB} 。1.2 角(angles)2. 凸区域 角和角的度量的概念是后面内容的绝对基础,在讨论这些概念之前,我们先介绍一下另一个重要的概念: 凸性(convex)。 凸区域(convex): 平面上的区域 \mathcal{R} ,若对于所有点 A,B\in \mathcal{R}: AB\subset \mathcal{R} , 则称该区域为凸区域(convex);否则称为非凸区域。 |
|
|
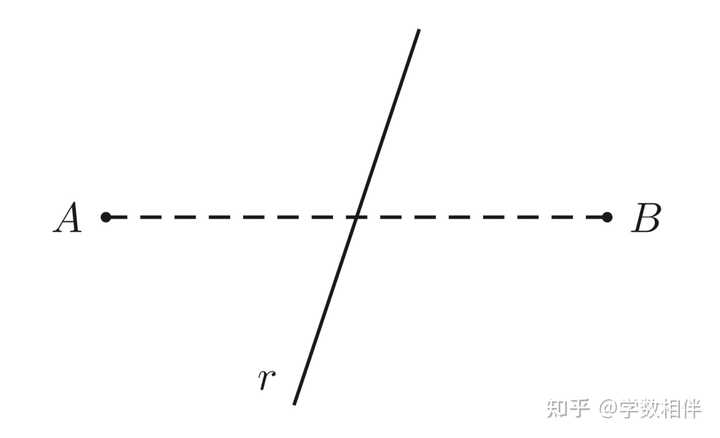
凸区域 非凸区域 非凸区域至少可以找到两个点 A,B\in \mathcal{R} : AB\not\subset \mathcal{R} 。 直线界限的闭合半平面(closed half-planes bounded by r): 平面的任意一条直线 r 将平面分为两个凸区域,称为直线 r 界限的闭合半平面(closed half-planes bounded by r)。 说明: 直线 r 可以被看成含在两个半平面中的任何一个中。若在两个半平面中分别选定一个点 A,B ,则必然有 AB\bigcap r \neq\emptyset ,也就是 AB 直线与界限必然相交。 |
|
|
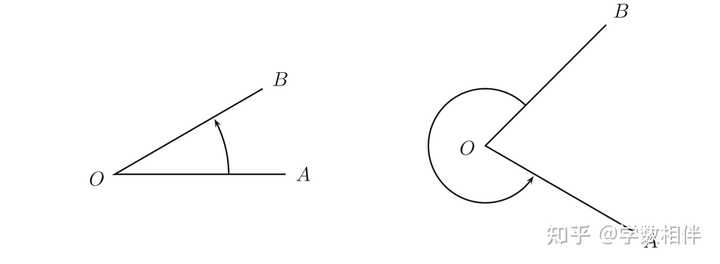
两半平面内的任意两点连线都与这两半平面分割线相交3. 角及角的度量 角(angle, angle region): 设 \stackrel{\rightarrow}{OA}, \stackrel{\rightarrow}{OB} 为平面内两个不同的射线(half-lines),这两条射线将平面分割为两个区域。则称这两个区域之一为顶点(vertex) O 和边(sides) \stackrel{\rightarrow}{OA}, \stackrel{\rightarrow}{OB} 的角或角区域。 |
|
|
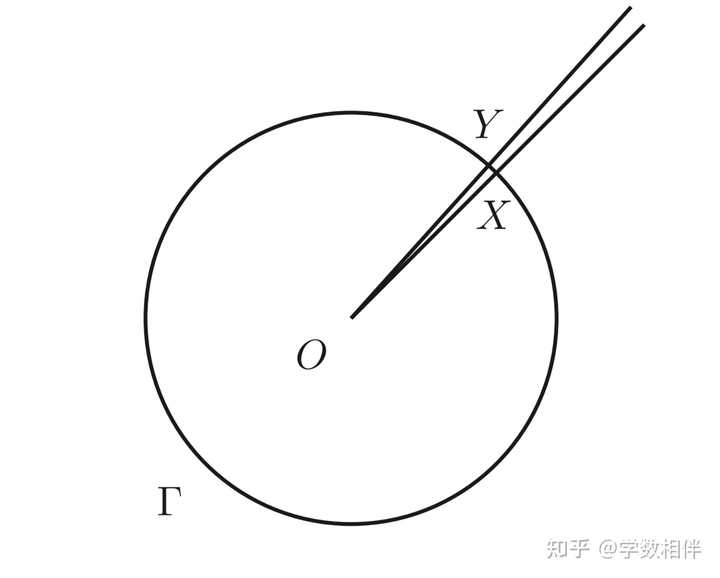
角(angle), 左侧为凸区域, 右侧为非凸区域 角可以是凸区域也可以是非凸区域,上面的角都可以记作 \angle AOB ,但是具体指代的是凸区域还是非凸区域,我们要根据上下文来确定。 角的度量(measure): 将圆 \Gamma(O, r) 分为360个相等的弧,取其中一个弧的两个端点 X,Y 与圆心所组成的角称为1度,这个度量记作 \widehat{XOY} = 1^\circ 。 |
|
|
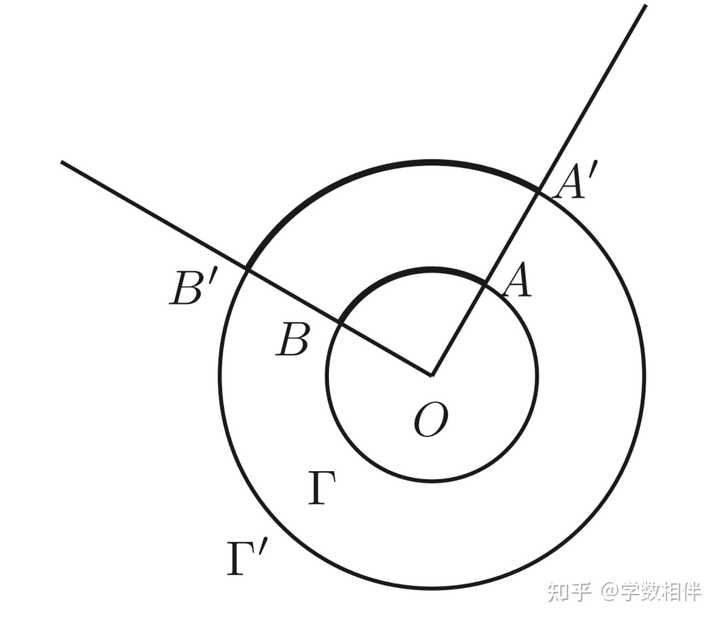
1弧度 注意: 对于这个定义,要保证其well-defined, 我们需要确定,角的这个度量与具体圆的半径 r 的选择无关。换句话说,用不同的半径划分后得到的其中一份都代表相同的度量,这点我们是通过下面的公理来说明的。 |
|
|
度数概念的良好定义 公理: 同样的两条以 O 为端点的射线隔两个圆得到的两个弧度数相等 \overset{\LARGE{\frown}}{AB} = \overset{\LARGE{\frown}}{A^\prime B^\prime} 。 根据度的定义: 完整圆对应于 360^\circ 。 接下来还有一个问题: 如何度量任意给定的角 \angle AOB 呢? |
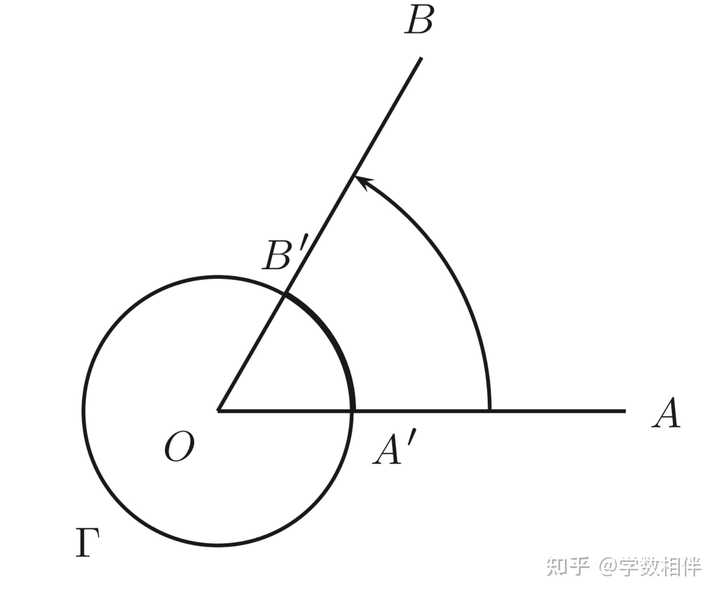
|
|
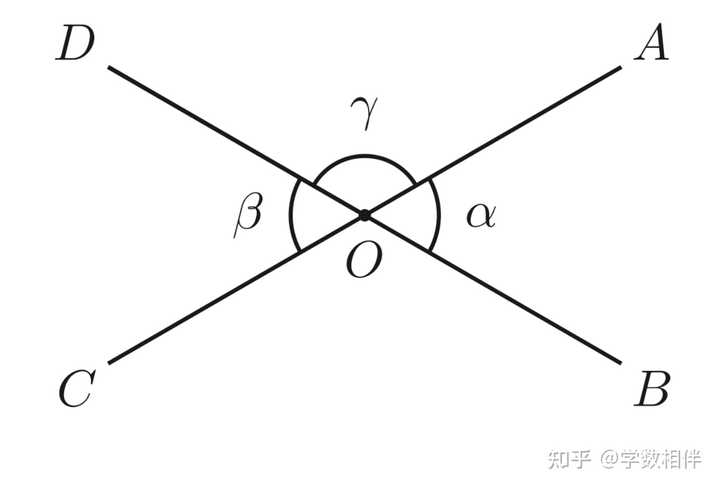
任意角的度量以 O 为圆心绘制一个圆 \Gamma , 该圆交 OA, OB 于对应的点 A^\prime, B^\prime 。计算弧 \overset{\LARGE{\frown}}{A^\prime B^\prime} 占圆 \Gamma 总长的比值。那么 \angle AOB 的度量 \widehat{AOB} 就等于 360^\circ 的那个比值倍。 例如,假如说弧 \overset{\LARGE{\frown}}{A^\prime B^\prime} 占圆 \Gamma 总长的比值为 1/6 , 那么,那么 \angle AOB 的度量 \begin{aligned}\widehat{AOB} = \frac{1}{6}\cdot 360^\circ = 60^\circ\end{aligned}\\ 注解1.6: 如果两个角的度量相等,那么这两个角相等。为了避免混淆的风险,我们对角度和它的度量用不同的记号: \angle AOB 表示射线 OA, OB 两个边所夹的角,而 \widehat{AOB} 总是表示角 \angle AOB 对应的度量(单位为度)。在具体上下文中,我们会用小写希腊字母表示角的度量。例如 \widehat{AOB} =\theta 表示 \angle AOB 的度量为 \theta 。4. 角的分类 半圆: 每个直径 AB 将圆平分为两个相同的部分,此时 \angle AOB 对应的度量为 180^\circ 。 通常来说,我们很少遇到角度数大于 180^\circ 的,除非明确说明,一般假设角度数都是说的是凸角 \angle AOB ,其度量为 0^\circ < \widehat{AOB} \leq 180^\circ 。 锐角(acute angle): \widehat{AOB} = 90^\circ 。 钝角(obtuse angle): \alpha, \beta 的度量之和为 90^\circ , 称这两个角互补 \alpha + \beta = 90^\circ 。 互余角 为complementary angles,互补角可以说supplementary angles。 对顶角(opposite angle, OPP), 如果两个角 \angle AOB, \angle COD 的两条边刚好是对应相反的两条射线,那么这两个角称为对顶角。 |
|
|
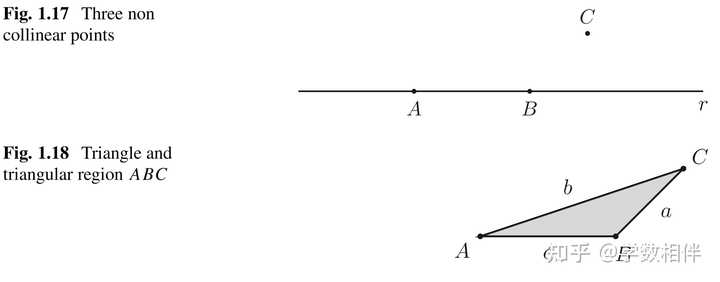
对顶角 命题1.9: 对顶角相等(Two opposite angles have equal measures)。 证明: \alpha + \gamma = 180^\circ = \beta + \gamma ,于是得到 \alpha = \beta 。 1.3 凸多边形(convex polygons)6. 共线和三角形 共线(collinear): 平面内三点 A,B,C , 如果 C\in \stackrel{\leftrightarrow}{AB} , 则说这三个点共线。 三角形(triangle): 平面内不共线的三个点 A,B,C 构成一个三角形。此时称这三个点为三角形的顶点(vertices);线段 AB, BC, CA 叫做三角形的三条边(sides, edges)。 三角区域(triangular region)对应于三角形 ABC 。 |
|
|
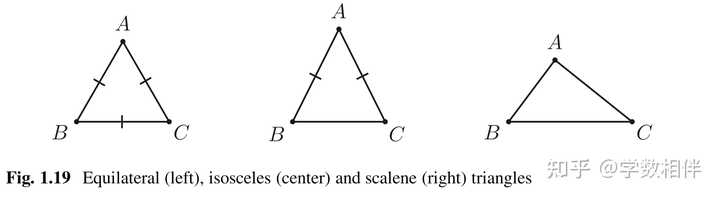
通常来说,如果不产生混淆的话,我们直接用三角形的三边长度做为它们对应的边,通常记号如上图所示 \overline{AB} = c,\overline{AC} = b,\overline{BC} = a 。 周长(perimeter): 三角形的三边长度之和称为三角形的周长。通常我们使用 p 表示半周长(semiperimeter) \bbox[10pt,border:1pt]{\begin{aligned}p = \frac{a+b+c}{2}\end{aligned}}\tag{1.1}\\ 三角形内角(interior angles): \angle A= \angle BAC, \angle B= \angle ABC, \angle C= \angle ACB , 或者 \widehat{A} = \widehat{BAC}, \widehat{B} = \widehat{ABC}, \widehat{C} = \widehat{BCA} 称为三角形的内角。 三角形的常见分类方法 按边长度来分类: 按照至少两边相等、任意两边都不相等来分类, 分为等腰三角形和不等边三角形。按内角的度量来分类: 按照最大角的度数是钝角、直角还是锐角来分。 定义1.10: 对于三角形 ABC 来说 等边三角形(equilateral): 如果 \overline{AB} = \overline{BC} = \overline{AC} , 则三角形 ABC 为等边三角形。 等腰三角形(isosceles): 如果 \overline{AB}, \overline{BC} ,\overline{AC} 至少有两个相等 , 则三角形 ABC 为等腰三角形。 不等边三角形(scalene): 如果 \overline{AB} \neq \overline{BC} \neq \overline{AC}\neq \overline{AB} ,则三角形 ABC 为不等边三角形。 注意: 等边三角形也是等腰三角形;但等腰三角形不一定是等边三角形。 |
|
|
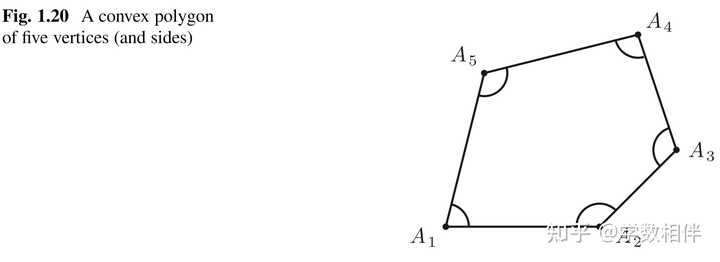
等腰三角形的底(basis): 等腰三角形 ABC , 相等的两边为 \overline{AB} = \overline{AC} , 那么 BC 边称为这个等腰三角形的底边。 对于等边三角形来说,任何一个边都是其底(basis);但是通常我们只称非等边的等腰三角形保留底的概念。 7. 凸多边形 根据三角形的定义,我们可以知道三角形是一种特殊的凸多边形。 |
|
|
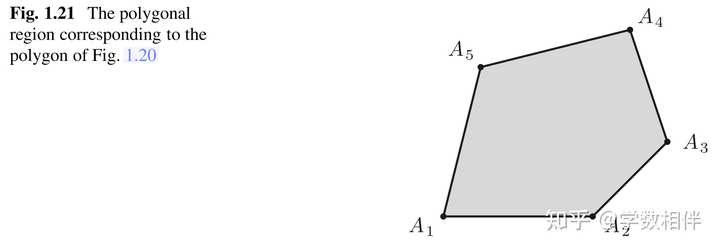
凸多边形(convex polygon), 设 n\geq 3 为自然数, A_1, A_2,\cdots, A_n 为平面内的 n 个不同的点,如果对于 1\leq i \leq n 下面两个条件满足(取 A_{n+1} = A_1 ): a) \overleftrightarrow{A_iA_{i+1}} 不包含任意其他的点 A_j 。 b) \overleftrightarrow{A_iA_{i+1}} 将其他点 A_j 都隔离在它自己确定的同一个半平面内。 那么就称 A_1A_2\cdots A_n 为凸多边形。 顶点(vertices): 点 A_1, A_2,\cdots, A_n 称为多边形的顶点。 边(sides): 线段 A_1A_2, A_2A_3, \cdots, A_nA_1 称为多边形的边。 周长(perimeter): 凸多边形所有边的和称为它的周长。 多边形区域(polygonal region): 对应于多边形 A_1A_2\cdots A_n 的多边形区域是平面的有界区域,其边界为多边形边的并集。 |
|
|
对于凸多边形同样有内角和外角的定义,内角对应的是凸角,外角与内角共一条边,另一边相反方向的射线为边。 |
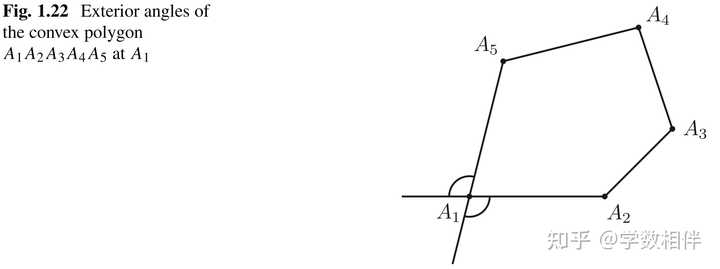
|
|
一般称凸多边形 A_1A_2\cdots A_n 为凸n-gon,具有n条边和n个顶点。 四边形(quadrilateral): n=4 。 五边形(pentagon): n=5 。 六边形(quadrilateral): n=6 。 七边形(heptagon): n=7 。 八边形(octagon): n=8 。 十边形(decagon): n=10 。 同样用大写字母 AB, BC, CD,DA 这些表示边。 命题1.12: 每个凸n-gon刚好有 \begin{aligned}\frac{n(n-3)}{2}\end{aligned} 条对角线。 证明: 三角形没有对角线, \begin{aligned}n=3: \frac{n(n-3)}{2} =0\end{aligned} , 无需证明。 对于 n\geq 4 , 我们可以连接 A_1 到其他的 n-1 个顶点 A_2, \cdots, A_n , 得到 n-1 条线段, 其中有两条 A_1A_2, A_1 A_n 为两条边,那么剩下的 n-3 条线段都是对角线( A_1A_3, \cdots, A_1A_{n-1} )。 因此对于任意一个顶点来说,我们都有 n-3 条对角线,于是将这些加起来就得到 n(n-3) 条线段,但是其中任意一条对角线都被重复计算两次,于是就得证结论。 第二章: 全等三角形 本章主要介绍三角形视为相同的充要条件集,从某种意义上来说,很快就会变得精确。在本章还讨论了欧氏几何的第五公理(平行公理),以及它的几个有趣的、重要的结论。其中最著名的是三角不等式。本章最后还介绍了集中特殊类型的四边形。 2.1 全等情形8. 全等概念 三角形等价(equivalence): 这是关于三角形中的等价关系,我们有特殊的名字,称为全等(congruence)。 全等三角形: 两个三角形,移动其中一个三角形的位置,保持不让其变形,如果能和第二个三角形完全重合,那么就称这两个三角形全等。这里的不变形移动包括: 平移、旋转、翻转等动作。 全等三角形具有顶点对应关系、边对应关系和角对应关系: 全等的两个三角形 ABC, A^\prime B^\prime C^\prime ,存在顶点的对应关系: A\leftrightarrow A^\prime, B\leftrightarrow B^\prime, C\leftrightarrow C^\prime\\ 因此也存在对应边和对应内角的相等: \left\{ \begin{array}{ll} \widehat{A} = \widehat{A^\prime}, \widehat{B} = \widehat{B^\prime}, \widehat{C} = \widehat{C^\prime}\\ \overline{AB} = \overline{A^\prime B^\prime},\overline{AC} = \overline{A^\prime C^\prime},\overline{BC} = \overline{B^\prime C^\prime} \end{array} \right.\\ 因为全等三角形是关于三角形的等价关系,因此具有等价关系的性质: 对称性(Symmetry): \Delta ABC\cong \Delta DEF\implies \Delta DEF\cong \Delta ABC 。前面的三角形可以移动与后面三角形重合,反过来后面三角形移动也可以与前面的三角形重合。 |
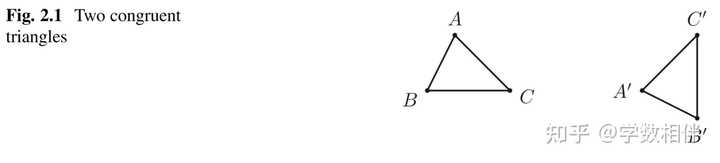
|
|
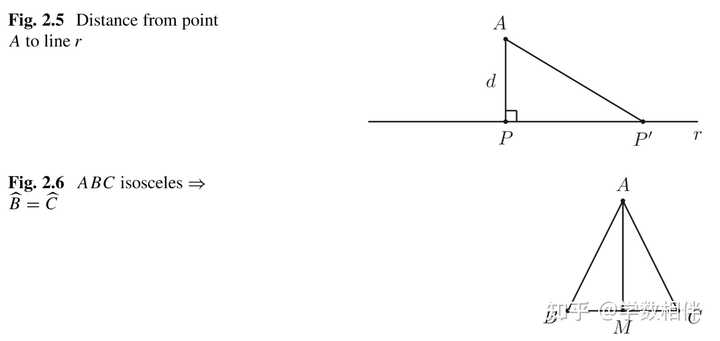
2. 传递性(transitivity): \left. \begin{array}{ll} \Delta ABC\cong \Delta DEF\\ \Delta DEF\cong \Delta GHI \end{array} \right\} \implies \Delta ABC\cong \Delta GHI\\3. 反身性(reflexivity): 当然 \Delta ABC\cong \Delta ABC , 这个是自然的,三角形与自身全等。 这就是关于等价关系需要满足的三条性质,全等是三角形中的一种等价关系。 三角形全等,记作 ABC \equiv A^\prime B^\prime C^\prime, ABC\cong A^\prime B^\prime C^\prime\\ 对应顶点 A\leftrightarrow A^\prime, B\leftrightarrow B^\prime, C\leftrightarrow C^\prime\\ 9. 边角边情形 有了全等的定义,我们需要给出一些方便应用的判别三角形全等的情形集合: 三角形全等情形(cases of congruence of triangles)。 首先来介绍第一种,边角边情形。 公理2.3(SAS全等情形): 如果两个三角形的两条边以及它们的夹角对应相等,那么这两个三角形全等。 \begin{aligned}\begin{equation} \left . \begin{aligned} \overline{AB}=\overline{A^\prime B^\prime}\\ \overline{AC}=\overline{A^\prime C^\prime}\\ \widehat{A} = \widehat{A^\prime} \end{aligned} \right\}\stackrel{SAS}{\implies} ABC\cong A^\prime B^\prime C^\prime \end{equation}\end{aligned}\\ 对应顶点: A\leftrightarrow A^\prime, B\leftrightarrow B^\prime, C\leftrightarrow C^\prime 。那么就可以得到: \widehat{B} = \widehat{B^\prime}, \widehat{C} = \widehat{C^\prime}, \overline{BC} = \overline{B^\prime C^\prime}\\ 10. 角边角情形 公理2.5(ASA全等情形): 如果两个三角形的两个角以及两个角所夹的边对应相等,则这两个三角形全等。 \begin{aligned}\begin{equation} \left . \begin{aligned} \widehat{A} = \widehat{A^\prime}\\ \overline{AB}=\overline{A^\prime B^\prime}\\ \widehat{B} = \widehat{B^\prime} \end{aligned} \right\}\stackrel{ASA}{\implies} ABC\cong A^\prime B^\prime C^\prime \end{equation}\end{aligned}\\ 对应顶点: A\leftrightarrow A^\prime, B\leftrightarrow B^\prime, C\leftrightarrow C^\prime 。那么就可以得到: \widehat{C} = \widehat{C^\prime}, \overline{AC} = \overline{A^\prime C^\prime}, \overline{BC} = \overline{B^\prime C^\prime}\\ 11. 边边边情形 公理2.7(SSS全等情形): 如果两个三角形对应的三条边相等,那么这两个三角形全等。 \begin{aligned}\begin{equation} \left . \begin{aligned} \overline{AB}=\overline{A^\prime B^\prime}\\ \overline{BC}=\overline{B^\prime C^\prime}\\ \overline{CA}=\overline{C^\prime A^\prime}\\ \end{aligned} \right\}\stackrel{SSS}{\implies} ABC\cong A^\prime B^\prime C^\prime \end{equation}\end{aligned}\\ 对应顶点: A\leftrightarrow A^\prime, B\leftrightarrow B^\prime, C\leftrightarrow C^\prime 。那么就可以得到: \widehat{A} = \widehat{A^\prime},\widehat{B} = \widehat{B^\prime},\widehat{C} = \widehat{C^\prime}\\ 值得注意的是,ASA和SSS全等情况可以由SAS情况推出,在下列意义下: 给定平面上的两个三角形,可以证明ASA或SSS的有效意味着这两个三角形满足SAS。 但是这里只是做下说明,忽略掉也没有任何问题。 我们还有推论2.22以及问题1中介绍的三角形全等的另外两个情况,这些情况都可以从 ASA, SSS 情形推导出来。 最后说明一点,如果两个三角形全等,并且不会产生混淆的情况下,我们可以省略它们顶点之间的对应关系。当然为了理解,我们每次都最好建立三角形全等检查时隐含的顶点对应关系。 2.2 全等应用12. 角平分线 角平分线(bisector): 给定一个角 \angle AOB , 它的角平分线就是射线 \overrightarrow {OC}: \ \widehat{AOC} = \widehat{BOC} 。 或者说 \overrightarrow {OC}\ \mathrm{bisects}\ \angle AOB\iff \widehat{AOC} = \widehat{BOC}\\ 假设角平分线存在,则唯一(不做证明)。 三角形 ABC 内角平分线(internal bisector)的概念: 就是对应的三个内角的角平分线与对边交点之间的线段称为内角平分线,三角形内角平分线对应三个顶点或三条边有三个内角平分线。 13. 线段中点 三角形中线(median): 三角形 ABC 三个顶点与对边中点的连线称为三角形的中线,三角形有三条中线。 14. 垂线 平面内两条线段垂直(perpendicular): 平面内两条直线 r,s 如果交于一点,并且在该点形成一个 90^\circ 的角,则称这两条直线垂直,记作 r\perp s 。 垂足(foot of perpendicular): 在 A\not\in r 的情形中, s\perp r, A\in s , 则 s,r 交点称为 A 到 r 的垂线的垂足。 备注2.12: 给定平面内的点 A 和直线 r ,则过 A 且垂直于 r 的直线唯一。 直线 r 外的点 A 到直线 r 的距离(distance)就是 \overline{AP} , 其中 P 即对应点 A 关于直线 r 的垂足。 后面我们会得到一个结论: 点 A 与直线 r 上的点构成的线段中垂线段最短。 三角形的高线(height, altitude): 顶点和对边垂足之间的线段称为高线。 |
|
|
15. 等腰三角形底角相等 命题2.13: 等腰三角形底角相等。 我们自行验证一下,只需要取底边的中线,利用 SSS 即可证得。 推论2.14: 等边三角形的三个内角相等。 这个直接由上面命题可推得,可以自行尝试一下,虽然简单,但是蛮有意思,也能锻炼对于理论的掌握。 2.3 平行(parallel)16. 共点和平行 共点(concurrent): 平面内两条直线,如果有共同点,则称它们共点(concurrent)。 平行(parallel): 平面内两条直线没有共同点,则称它们平行(parallel)。 |

|
|
17. 三角形外角不等式 接下来需要了解如何通过直线外一点绘制该直线的平行线。为此(to this end), 我们需要先介绍一下接下来的辅助结论: 外角不等式(exterior angle inequality)。 引理2.15: 三角形外角大于非相邻内角。 |
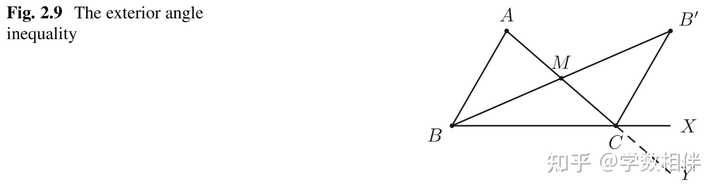
|
|
证明: 三角形 ABC ,取 AC 中点 M ,并做射线 BB^\prime 使得 M 为 BB^\prime 的中点。 利用对顶角和 SAS 全等情形,我们很容易证得 \widehat{B^\prime CA} = \widehat{B^\prime CM} = \widehat{BAM} = \widehat{BAC} \\">\widehat{XCA} > \widehat{B^\prime CA} = \widehat{B^\prime CM} = \widehat{BAM} = \widehat{BAC} \\同理我们还可以证明 \widehat{ABC}">\widehat{YCB} > \widehat{ABC} 。 # 18. 平行线公设 欧几里得在《几何原本》中将平行线公设作为第五公设。然而很多数学家,从古典到近代早期,都试图想从其他四个公设来推导这个公设,想把它作为一个定理。但是很可惜,所有都是徒劳。 在19世纪,匈牙利数学家János Bolyai和俄罗斯数学家Nikolai Lobatchevsky独立工作,表明确实有必要将平行作为一个公设。更准确的说,如果承认平行公理,我们就得到欧氏几何;如果不承认平行公理,就得到另一种类型的几何--非欧几何。后者承认过直线外一点可以有无数条直线与该直线平行,比较典型的就是球面的例子。 公设2.17(第五公设): 平面内给定一条直线 r 和给定一个点 A \not\in r , 存在唯一的过该点 A 且平行于该直线 r 的直线。 在尺规作图2.8中我们介绍了一种稍微复杂的绘制平行线的方法,稍后我们还会介绍更简单的绘制平行线的方法。对于两条直线平行,我们记作 r\parallel s 。 19. 内错角和同旁内角 我们有了欧几里德的第五公设,我们就可以得到欧氏几何中的一些重要结论。 |

|
|
平面内给定三条直线 r,s,t ,使得直线 t 与直线 r,s 分别交于两个不同的点 A,B ,如山图所示。 内错角(alternate interior angles): 比如上图中的角 \alpha,\beta 。 同旁内角(consecutive interior angles): 比如上图的角 \alpha,\gamma 。 推论2.18: 使用上图2.11中的记号, 我们有 r\parallel s\iff \alpha = \beta \iff \alpha + \gamma = 180^\circ\\ 说明: 构造平行线的过程用的是内错角相等。换句话说内错角相等两直线平行。而推论只需要说明同旁内角互补即可说明两直线平行,反之亦然。20. 三角形内角和 |

|
|
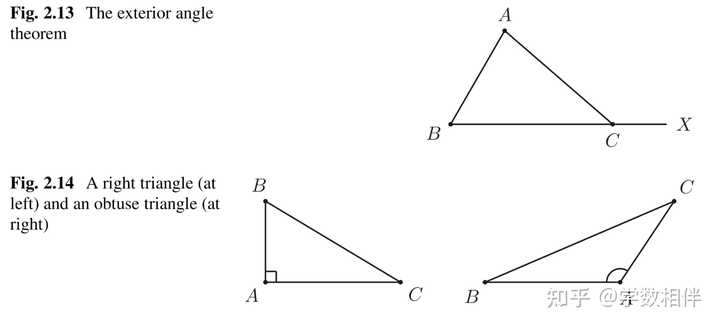
定理2.19: 三角形内角和为 180^\circ 。 只需要过其中一点作对边的平行线即可利用推论2.18得到该结论。 推论2.20: 等边三角形的每个内角为 60^\circ 。 推论2.21(外角定理exterior angle theorem): 三角形中,任意一个角对应的外角等于另外两个不相邻的内角之和。 |
|
|
定理2.19也让我们可以根据内角的度量来分类三角形。因为它能保证在一个三角形中,只有一个内角大于等于 90^\circ 。我们只需要利用反证法即可证得。 锐角三角形(acute triangle)有三个锐角。直角三角形(right triangle)只有一个直角。钝角三角形(abtuse triangle)只有一个钝角。直角三角形,直角对边称为斜边(hypotenuse), 直角边称为腿(legs)。21. 角角边情形 推论2.22(AAS全等情形): 两个内角及其中一个角的对边对应相等的两个三角形全等。 |

|
|
\begin{aligned}\begin{equation} \left . \begin{aligned} \widehat{A} = \widehat{A^\prime}\\ \widehat{B} = \widehat{B^\prime}\\ \overline{BC}=\overline{B^\prime C^\prime} \end{aligned} \right\}\stackrel{AAS}{\implies} ABC\cong A^\prime B^\prime C^\prime \end{equation}\end{aligned}\\ 对应顶点: A\leftrightarrow A^\prime, B\leftrightarrow B^\prime, C\leftrightarrow C^\prime 。那么就可以得到: \widehat{C} = \widehat{C^\prime}, \overline{AC} = \overline{A^\prime C^\prime}, \overline{AB} = \overline{A^\prime B^\prime}\\ 证明: 这个命题直接利用三角形内角和为180度,然后转换为 ASA 情形即可。 同样关于AAS全等的情况,假设我们知道三角形的一边的长度和两个内角的度量,其中一个内角与给定边相对(图2.15)。使用尺规作图构造三角形的问题将在例2.34中讨论。 2.4 三角形不等式 本节主要介绍三角形中两边之和大于第三边。当然两边之差小于第三边直接由不等式性质可推得。 22. 大角对大边 命题2.23: 大角对大边。若三角形 ABC 有 \widehat{C} ">\widehat{B} > \widehat{C} , 那么 \overline{AB}">\overline{AC} > \overline{AB} 。 |
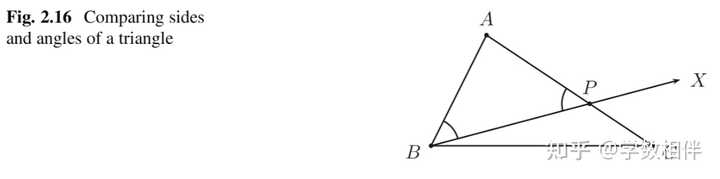
|
|
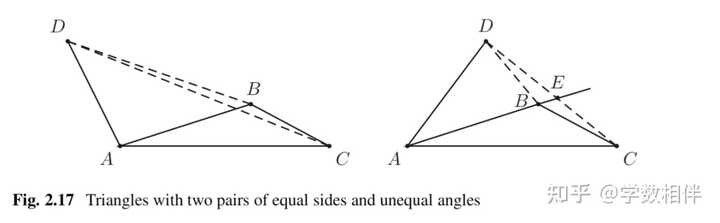
证明: 因为 \widehat{C} ">\widehat{B} > \widehat{C} ,那么可以可以从 B 点画一条射线 \overrightarrow{BX} , 让该射线穿过三角形 ABC 内部,并且满足 \begin{aligned}\widehat{CBX} =\frac{1}{2}(\widehat{B} - \widehat{C})\end{aligned}\\ 并设这条射线与 AC 交于点 P 。 则有 \begin{aligned} \widehat{APB} &=\widehat{CPB} + \widehat{C} \\&=\frac{1}{2}(\widehat{B} - \widehat{C}) + \widehat{C} \\&=\frac{1}{2}(\widehat{B} + \widehat{C}) \end{aligned}\\ 而 \begin{aligned} \widehat{ABP} &=\widehat{B} - \widehat{CBX} \\&=\widehat{C}+\frac{1}{2}(\widehat{B} - \widehat{C}) \\&=\frac{1}{2}(\widehat{B} + \widehat{C}) \end{aligned}\\ 因此得到 \begin{aligned} \widehat{APB} = \widehat{ABP} \end{aligned}\\ 三角形 ABP 为等腰三角形, ABC 中 \widehat{A} \geq 90^\circ , 那么 \overline{BC} 是最大边。特别的,在直角三角形中,斜边是最大边。 证明: 因为 \widehat{A} \geq 90^\circ ,根据三角形内角和为180度,足以说明 \angle A 为最大角,因此它所对的边为最大边。# 推论2.25: 两个三角形如果两对边对应相等,则这两组边所夹角越大,所对的对边长越长。 设 ABC, A^\prime B^\prime C^\prime 为两个三角形,其中 \overline{AB} = \overline{A^\prime B^\prime} , \overline{AC} = \overline{A^\prime C^\prime} , 如果 \widehat{BAC} < \widehat{B^\prime A^\prime C^\prime} , 则 \overline{BC} < \overline{B^\prime C^\prime} 。 |
|
|
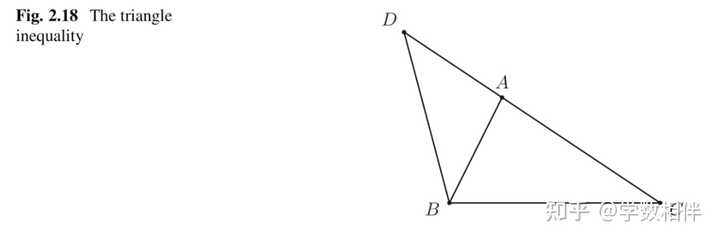
证明: 直线 \overleftrightarrow{AC} 确定了两个半平面,我们选择包含 B 点的那个半平面 \alpha 。 在半平面 \alpha 中取一点 D ,使得 \widehat{DAC} = \widehat{B^\prime A^\prime C^\prime} 且 \overline{AD} = \overline{A^\prime B^\prime} (也就是把两个三角形放在一起,全等)。 很容易利用 SAS 证明 \Delta DAC\cong \Delta B^\prime A^\prime C^\prime ,因此 \overline{DC} = \overline{B^\prime C^\prime} 。 我们只需要证明 \widehat{DBC} > \widehat{B D C} 即可。 而这个时候有两种情况需要考虑: 点 A, D 是位于直线 BC 同侧还是两侧。 (i) 点 A, D 是位于直线 BC 同侧(图2.17左图)。 因为\Delta ABD 是底边为 BD 的等腰三角形,于是就有 \widehat{DBA} = \widehat{BDA} 。 而有 \widehat{DBA}">\widehat{DBC} > \widehat{DBA} , \widehat{BDC} ">\widehat{BDA}> \widehat{BDC} , 因此得证 \widehat{B D C} ">\widehat{DBC} > \widehat{B D C} 。 (ii) 点 A, D 是位于直线 BC 两侧(图2.17右图), 要证明 \widehat{B D C} ">\widehat{DBC} > \widehat{B D C} , 它们两个在同一个三角形中,一个三角形中只能有一个是钝角,所以只需证明前者为钝角即可。设 \overleftrightarrow{AB} 交 CD 于点 E 。 因为\Delta ABD 是底边为 BD 的等腰三角形,因此可得到 \widehat{DBE} > 90^\circ 为钝角。 而 \widehat{DBE} ">\widehat{DBC} = \widehat{DBE} + \widehat{EBC} > \widehat{DBE} , 更是钝角。 # 23. 三角形不等式 定理2.26: 任何三角形中,两边之和大于第三边。 |
|
|
证明: 设 \Delta ABC , 按照之前三角形的符号约定,我们只需要证明 CA 到 D ,使得 \overline{AB}=\overline{AD} ,连接 DB 。 于是就有 \overline{CD} = \overline{CA} + \overline{AD} =b+c 。要证 \overline{BC} < \overline{CD} 。 根据大角和大边关系,我们只需要证明 \begin{aligned}\begin{equation} \left . \begin{aligned} \widehat{DBC} = \widehat{DBA} + \widehat{CBA}\\ \widehat{DBA} = \widehat{BDA} = \widehat{BDC} \end{aligned} \right\}\implies \widehat{BDC} < \widehat{DBC} \end{equation}\end{aligned}\\ 得证。 # 说明: 三角形不等式的常见换元法应用说明。 设 a,b,c 为给定三角形的三条边,那么就可以得到三角不等式 c, a+c > b, b+c>a\\">a+b > c, a+c > b, b+c>a\\ 那么,反过来,如果有三个实数满足上面的不等式关系,那么一定可以构造一个以这三个实数为边长的三角形。 很多情况下,我们三角形换元法的原理就来自这里。 24. 三角形内点不等式 例2.27: 若 P 是三角形 ABC 内的一点,则有 (a) \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC} (b) \overline{PA}+ \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC}+ \overline{BC} |

|
|
证明: a) 利用三角形不等式可证得, 延长 BP 交 AC 于 Q 点。 在 \Delta PQC 中 \overline{PB} + \overline{PC} < \overline{PB}+ \overline{PQ}+\overline{QC} = \overline{BQ}+\overline{QC}。 在 \Delta ABQ 中 \overline{PB} + \overline{PC} < \overline{BQ}+\overline{QC} < \overline{AQ}+\overline{AB} + \overline{QC}。 也就是 \overline{PB} + \overline{PC} < \overline{AQ}+\overline{AB} + \overline{QC} < (\overline{AQ}+ \overline{QC})+\overline{AB} , \overline{AQ}+ \overline{QC} = \overline{AC} , 于是证得 \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC} 。 b) 利用a)结论,我们分别可得到 \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC}\\ \overline{PA} + \overline{PB} < \overline{AC} + \overline{BC}\\ \overline{PA} + \overline{PC} < \overline{AB} + \overline{BC}\\ 左右对应相加即得: 2(\overline{PA}+ \overline{PB} + \overline{PC}) < 2(\overline{AB} + \overline{AC}+ \overline{BC}) , 于是得证。 # 25. 将军饮马 |

|
|
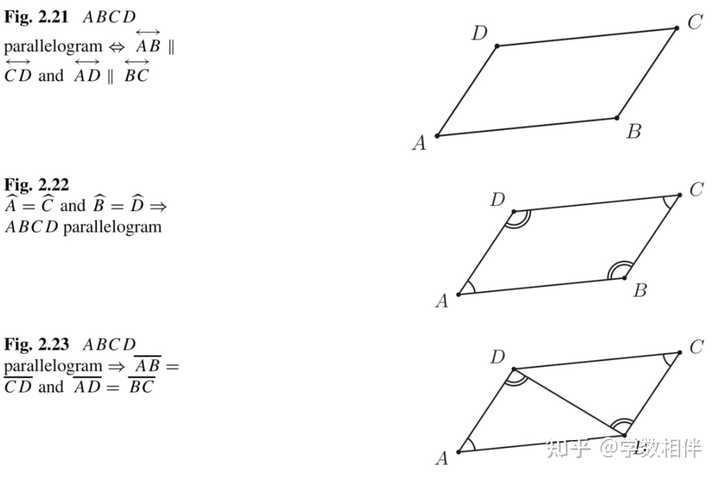
例2.28: 如图2.20, 使用尺规作图找一个点 P\in r 使得 \overline{PA} + \overline{PB} 尽可能的小。 传说亚历山大城有一位精通数学和物理的学者,名叫海伦。一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:从A地出发到河边饮马,然后再到B地,求怎样走使路线最短,并且求如何确定饮马的地点。提起路线最短的问题。将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,求怎样走才能使路程最短。这个问题的解决并不难,据说海伦略加思索就解决了它. 从此,这个被称为“将军饮马”的问题广泛流传. 解: 用尺规作图标记出点 A 关于直线 r 的对称点 A^\prime 。我们要求的是 \overline{PA} + \overline{PB} 的最小值问题。 而 \overline{PA} = \overline{PA^\prime} , 因此问题转换为求 \overline{PA^\prime} + \overline{PB} 的最小值问题。 对于定点 A^\prime, B 来说,连接两点的直线段距离最短(三角不等式的结论)。连线与直线 r 的交点 Q 即为所求。 2.5 特殊四边形(special quadrilaterals) 在本节中,我们开始对凸四边形的几何进行系统研究。在各种特殊的凸四边形类型中,最主要的肯定是平行四边形。 26. 平行四边形(parallelogram) 定义2.9: 两组对边都平行的凸四边形称为平行四边形。 稍后我们将讨论一些定义平行四边形的等价方法。我们需要将这些结论视为平行四边形的显著特性,后面我们会反复使用它们。 27. 平行四边形等价定义 |
|
|
命题2.30: 凸四边形为平行四边形当且仅当它的对角相等。 说明: 关于平行四边形对角相等,可以利用平行同旁内角互补,可以推出对角相等,这是平行四边形的性质定理。 而反过来,如果对角相等,我们可以利用四边形内角和为 360^\circ 证得同旁内角互补,证得对边平行。 命题2.31: 凸四边形为平行四边形当且仅当它的两组对边相等。 正向可以用角角边判定三角形全等来证得,这是平行四边形性质定理。 反向可以利用边边边判定三角形全等来得到对顶角相等,然后用命题2.30可证得。 命题2.35: 凸四边形为平行四边形当且仅当对角线互相平分。 |

|
|
证明: 若 ABCD 为平行四边形, M 为对角线交点,如上图所示。 ASA 可证得 \Delta ABM\cong \Delta CDM , 于是可证得 \overline{AM} = \overline{CM}, \overline{BM} = \overline{DM} 。 反过来,若 ABCD 对角线互相平分,我们可以使用 SAS 证得 \Delta ABM\cong \Delta CDM , 得到 \overline{AB} = \overline{CD} 。同理可得 \overline{BC} = \overline{AD} ,于是得证四边形 ABCD 是平行四边形。 # 28. 三角形中位线(midsegment) 中位线(midsegment): 三角形连接两边中点的线段称为中位线。三角形有三条中位线。 |

|
|
上图展示了三条中位线,其中三角形 \Delta MNP 称作中位三角形(midial triangle)。 命题2.36: 三角形中位线平行于底边且长度为底边的一半。 |
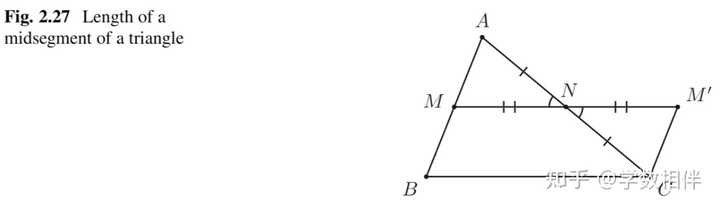
|
|
证明: 延长 MN 并取点 M^\prime: \overline{MN} = \overline{NM^\prime} ,如上图所示。 则 \Delta AMN\cong \Delta CM^\prime N(SAS)\implies \overline{M^\prime C}= \overline{MA},\widehat{M^\prime CN} = \widehat{MAN} ,于是 \overleftrightarrow{M^\prime C}\overset{\parallel}{=}\overleftrightarrow{AM} 。 而 \overline{AM}=\overline{MB} , 因此有 \overleftrightarrow{M^\prime C}\overset{\parallel}{=}\overleftrightarrow{MB}\iff MBCM^\prime 为平行四边形。而 \overline{MN} = \overline{NM^\prime} , 因此就有 \overline{MN}\overset{\parallel}{=}\frac{1}{2}\overline{BC}\\ 29. 三角形重心(barycenter) 三角形中线(median): 连接顶点到对边中点的线段称为三角形的中线。三角形有三条中线,三条中线交于一点,这一点称为三角形的重心(barycenter)。关于三条中线交于一点,可以利用平行四边形性质得到。 命题2.38: 三角形三条中线交于一点,这点称为重心。重心将中线一分为两段,比例为2:1。 |

|
|
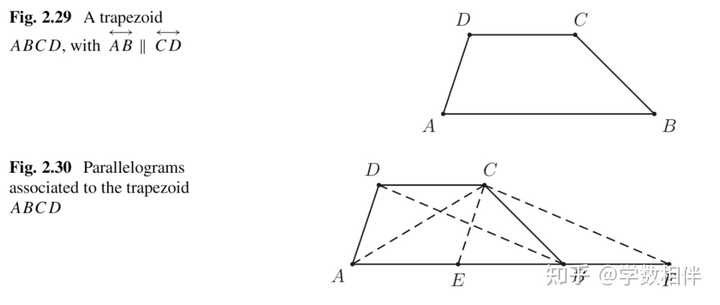
证明: 设 N,P 分别为 \Delta ABC 的两条边 AC,AB 的中点,设 BN\bigcap CP = \{G_1\} , 如上图所示。 分别取 BG_1,CG_1 的中点 S,T 。 因为 PN 是 \Delta ABC 相对于边 BC 的中位线,而 ST 是 \Delta G_1BC 相对于边 BC 的中位线, 它们都等于 \overline{BC} 的一半,因而就有 \overline{PN} = \overline{ST} 。 再者,中位线平行于对应底边,则有 \overleftrightarrow{NP}\parallel \overleftrightarrow{ST} 。 于是我们得到四边形 PNTS 为平行四边形。再利用平行四边形对角线互相平分,我们就可以得到 \overline{PG_1} = \overline{TG_1}, \overline{NG_1} = \overline{SG_1} , 再者 S,T 为 BG_1,CG_1 的中点。 于是就证得结论的第二部分 \overline{BG_1} = 2\overline{G_1N}, \overline{CG_1} = 2\overline{G_1P} 。 剩下的就是证明三条中线交于一点,我们只需要证明另外一条中线也过点 G_1 即可。 同理可设 M 为 BC 的中点, AM,BN 交于点 G_2 , 同样我们可以得到 G_2 将 AM,BN 分为2:1两段,于是就可以得到: \overline{BG_1} = 2\overline{G_1N}, \overline{BG_2} = 2\overline{G_2N} 。这就证得了 G_1 = G_2 。 # 约定一下: 使用 G 表示 \Delta ABC 的重心。 三角形重心是一个很重要的概念。三角形还有其他的心,比如说外心(circumcenter), 内心(incenter), 正交中心(orthocenter)。这些将在3.2节中学习。 30. 梯形(trapeziod, trapzium) 对边平行且相等的四边形为平行四边形;但是四边形的两组对边平行也可以不相等,这样就得到另外一种特殊四边形,梯形。显然平行四边形是特殊的梯形,而梯形未必是平行四边形。 |
|
|
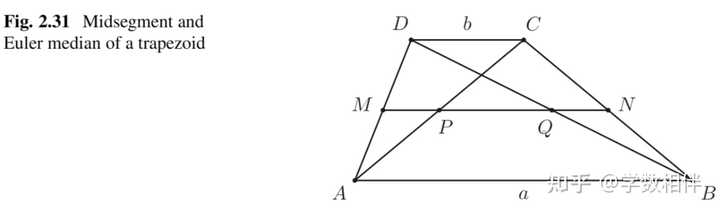
梯形中,平行的两条边称为底边(bases),也就是我们常说的梯形的上底和下底(larger, smaller bases)。另外两条边称为梯形的腰(legs)。 当处理如图2.29所示的梯形 ABCD 中的几何构造问题时,经常可以观察到(参见图2.30),如果 E,F 是线 \overleftrightarrow{AB} 上的点,其中 ADCE, BDCF 是平行四边形,那么: 三角形 BEC : \overline{BE} = \overline{AB} - \overline{CD}, \overline{CE} = \overline{AD} , \widehat{BCE} = 直线 \overleftrightarrow{AD}, \overleftrightarrow{BC} 所形成的夹角。三角形 ACF : \overline{AF} = \overline{AB} + \overline{CD}, \overline{CF} = \overline{BD} , \widehat{ACF} = 直线 \overleftrightarrow{AC}, \overleftrightarrow{BD} 所形成的夹角。31. 欧拉中线 在我们继续之前,我们需要对梯形设置更多的约定,即: 梯形中线: 连接腿中点的线段是梯形的中段。 欧拉中线: 而连接对角线中点的线段则是欧拉中线。 接下来的命题教我们如何根据梯形底的长度计算这些线段的长度。 命题2.40: 梯形 ABCD 的两个底边 AB,CD , 两腰 AD,BC 。设 P,Q 分别为两条对角线 AC,BD 的中点,则: (a) M,N,P,Q 共线,且 \overleftrightarrow{MN} \parallel \overleftrightarrow{AB}, \overleftrightarrow{CD} 。 (b) \begin{aligned}\overline{MN} = \frac{1}{2}(\overline{AB} + \overline{CD}), \overline{PQ} = \frac{1}{2}(\overline{AB} - \overline{CD})\end{aligned} 。 |
|
|
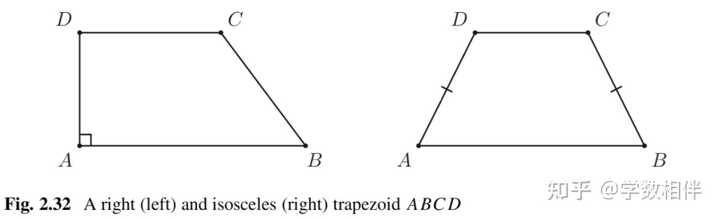
证明: 我们只需要知道 \overline{MN} = \overline{MP} + \overline{PN},\overline{PQ} = \overline{PN} + \overline{QN} 即可得证。 直角梯形(right): 其中一个底角为直角的梯形称为直角梯形。 等腰梯形(isosceles): 腰相等的梯形称为等腰梯形。 |
|
|
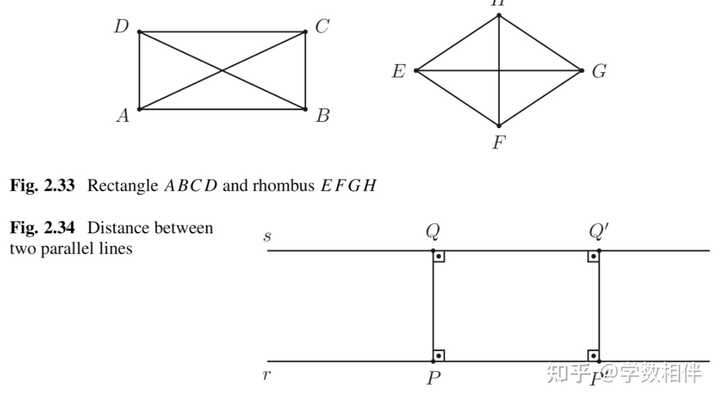
32. 矩形(rectangle)和菱形(rhombus) 为了完成我们对更基本的四边形特殊类型的研究,现在让我们看看矩形和菱形。如果凸四边形的所有内角都具有相等的度量,则凸四边形是矩形。 |
|
|
四边形可以分成两个三角形,内角和为360°,因此我们得出结论,当且仅当其四个内角的度量等于90°时,凸四边形是矩形。如果其四条边的长度都相等,则凸四边形就是菱形。图2.33显示了矩形和菱形的示例。 由于矩形的两侧总是平行的(因为它们都垂直于其他两侧),我们得出结论,每个矩形都是平行四边形。另一方面,命题2.31保证每个菱形也是平行四边形。 上述讨论使我们能够定义两条平行线之间的距离。为此,首先注意,如果 r\parallel s 是平行线,那么(参见推论2.18)线 t\perp r ,当且仅当 t\perp s 。 定义2.41: 平行线 r,s 之间的距离(distance)为 PQ, P\in r, Q\in s, \overleftrightarrow{PQ}\perp r,s 。 平行线之间的距离相等,可以由矩形的性质推得。 命题2.43: 平行四边形为矩形当且仅当对角线相等。 |

|
|
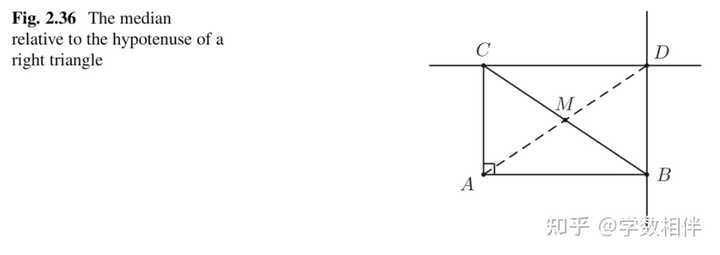
证明: 若 ABCD 为矩形,则四个角均为 90^\circ ,另外矩形也是平行四边形,因此对边相等,根据 SAS 可证全等 \Delta ABD\cong \Delta CDB ,得到对角线相等 \overline{AC} = \overline{BD} 。 反过来,如果对角线相等,平行四边形对边相等,由 SSS 可证得全等,于是平行四边形对角相等,而对角互补,立即得到四个角均为 90^\circ ,于是得证平行四边形为矩形。 # 推论2.44: 直角三角形斜边中线长度为斜边的一半。 |
|
|
证明: 直角三角形作直角顶点关于斜边中点的对称点,我们得到矩形,结论立得。 # 命题2.46: 平行四边形为菱形(rhombus)当且仅当它的对角线互相垂直。 证明: 菱形四条边相等,可以由 SSS 得到全等,于是得到关于对角线所得到的四个角相等,因此都是 90^\circ 。 反过来,如果平行四边形 EFGH 对角线互相垂直,又因为平行四边形对角线互相平分,那么对角线既是高线又是中线。我们很容易得到邻边相等的结论,于是就得到这种平行四边形是菱形。 33. 正方形(square) 最后再看看正方形,一种特殊的凸四边形,它同时是矩形和菱形。因此正方形具有相等的边和内角,另外它对角线也相等且垂直,交于中点,并且与正方形的边成 45^\circ 角。 备注2.47: 梯形(trapezoids) \mathcal{T} , 平行四边形(parallelograms) \mathcal{P} , 矩形(rectangles) \mathcal{R}, 矩形(rhombuses) \mathcal{L}, 正方形(rhombuses) \mathcal{Q}, 那么就有下面的关系: \mathcal{R} \bigcup \mathcal{L} \subset \mathcal{P} \subset \mathcal{T}\\ \mathcal{R}\bigcap \mathcal{L} = \mathcal{Q}\\ 这里包含关系都是严格包含。 14. 尺规作图1.1 线段长度比较 |

|
|
用圆规一脚固定在A点,然后调整圆规张开的角度,使得另一脚刚好落在B点。保持圆规的张开角度,然后将其中一脚固定在C点,另外一脚绘制一个圆弧交CD于E点,这样 \overline{CE}= \overline{AB} 。比较 \overline{CE}= \overline{AB} 和 \overline{CD} 的长度。1.2 两线段长度和及线段长度的自然倍数 |

|
|
尺规作图: 绘制线段 \overline{EF} = \overline{AB} + \overline{CD}, \overline{GH} = 3\overline{AB} 。 用直尺绘制直线 r 。在 r 上选择一个点 X , 平移线段 AB 到直线 r 上,获得线段 EX ,使得 \overline{EX} = \overline{AB} 。平移线段CD到直线r上,起点位于X点,获得点F,使得 \overline{XF} = \overline{CD}, X\in EF 。那么线段EF长度就等于 \overline{AB} + \overline{CD} 。用上面的类似的方法,我们可以得到线段 \overline{GH} = 3\overline{AB} = \overline{AB} + \overline{AB} + \overline{AB} 。1.3 绘制圆 |

|
|
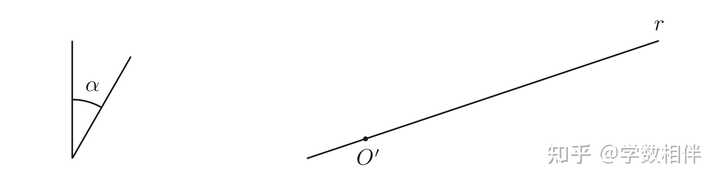
用圆规测出所给线段 l 长度,固定夹角。然后选择一个圆心O,以 l 长度确定一个点 A ,使得 \overline{OA} 等于所给半径长度。然后让圆规另一角旋转360度,得到所要绘制的圆。1.4 绘制给定大小的角 三角形全等的 SSS 命题会证明这里的步骤是合理的。 例1.7: 尺规作图绘制给定大小的角 绘制一个角,顶点为 O^\prime , 其中一条边在 r 上,且其度量为 \alpha : |
|
|
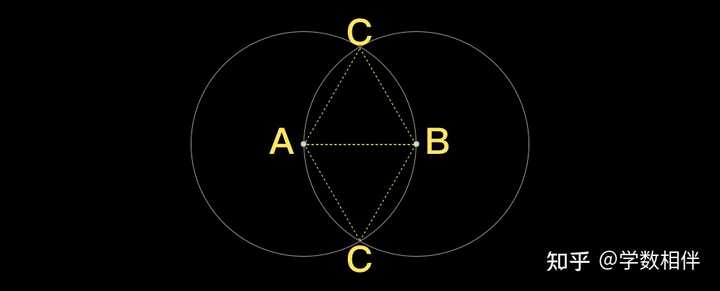
在给定的角上,以顶点为圆心绘制一个任意半径 R 的圆,交这个角的两条边于两个点 X,Y 。然后再以 O^\prime 为圆心, R 为半径绘制一个圆,交直线 r 于一点,记作 Y^\prime 。然后以 Y^\prime 为圆心,绘制半径为 \overline{XY} 的圆 \Sigma(Y^\prime, \overline{XY}) ,与圆 \Gamma(O^\prime; R) 交于点 X^\prime 。则得到角 \angle X^\prime O^\prime Y^\prime 就是度量为 \alpha 的角,即所求。2.1 绘制等边三角形 例2.1: 尺规作图,绘制等边三角形 ABC ,腰为给定线段的长度 l |

|
|
平面内任意选定一个点 A 。使用圆规以 A 为圆心, l 为半径绘制一个圆。在圆上任意选定一个点作为 B 。然后使用圆规再次以 B 为圆心, l 为半径绘制另一个圆。然后两个圆之间有两个交点,随便选哪一个作为 C 点均可,这个时候得到所要的等腰三角形 ABC 。 |
|
|
2.2 边角边绘制三角形 尺规作图,绘制给定三角形 ABC 的全等三角形,已知条件 \overline{AB} = a, \overline{AC} = b,\widehat{A} = \gamma 。 换句话说已知三角形两条边和它们的夹角,让我们用尺规作图绘制一个全等的三角形。 |

|
|
平面内选择一个点 C , 绘制一条射线 \overrightarrow{CX} 。绘制一个角 \widehat{XCY} = \gamma ,这样就确定了另一条射线 \overrightarrow{CY} 。分别在两条射线 \overrightarrow{CX}, \overrightarrow{CY} 上取两个点 B,A: \overline{AC} = b, \overline{BC} = a 。 得到的三角形 ABC 即为所求。 |
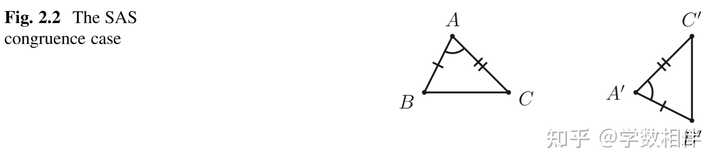
|
|
多次执行上述构造步骤,我们会发现,选择不同的点 C ,对于 \angle XCY 点边可以选择两个不同的方向,得到的不同的三角形 ABC 都是全等的。这个例子就给出了我们一个全等的情形,也就是 SAS 情形。 2.3 角边角绘制三角形 例题2.4: 已知两个角 \widehat{B} = \beta, \widehat{C} = \gamma 和一条边 \overline{BC} ,尺规作图绘制全等三角形 |

|
|
绘制一条直线 r , 并在上面取两点 B,C: \overline{BC}=a 。绘制射线 \overrightarrow{BX}: \widehat{CBX} = \beta 。在直线 r 划分的两个半平面,包含点 X 的一面绘制一条射线 \overrightarrow{CY}: \widehat{BCY} = \gamma 。标记两条射线 \overrightarrow{BX}, \overrightarrow{CY} 的交点为 A 。 则三角形 ABC 即为所求。 同样,我们可以重复上面的步骤绘制多个这样的三角形,让它们位置和方向不同,这些三角形是全等的。于是就激发我们得到第二个三角形全等的情形,称为 ASA 情形。 2.4 边边边绘制三角形 例2.6: 已知三角形 ABC 的三条边长 \overline{AB} = c, \overline{AC} = b, \overline{BC} = a , 用尺规作图绘制另一个三角形三边与它们对应相等。 |

|
|
绘制线段 \overline{BC} =a 。然后分别以 B 为圆心绘制半径为 c 的圆、以 C 为圆心绘制半径为 b 的圆。记两个圆的两个交点之一为点 A 。 则所得三角形即为所求。 同样,我们可以重复上述步骤多绘制几个三角形,这些三角形也是全等的,于是就激发了我们关于全等三角形情形的第三种情况。 2.5 绘制角平分线 |
|
|
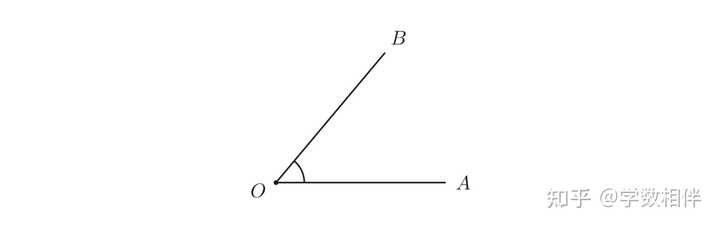
以 O 为圆心绘制半径为任意长度 r 的圆,标记圆与角的两条边的交点 X,Y ,它们分别在射线 \overrightarrow {O A}, \overrightarrow {OB} 上。选择一个长度 \frac{1}{2}\overline{XY}">s > \frac{1}{2}\overline{XY} , 然后分别以 X,Y 为圆心, s 为半径绘制两个圆弧交于点 C (与 O 不重合)。 |
|
|
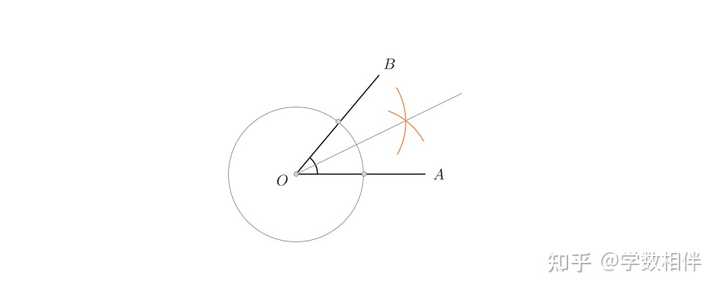
如上图所示,所得的射线 \overrightarrow{OC} 即为所求。 思考一下,这里的做法为什么有效? (提示 SSS 全等情形。) 结合 SSS, SAS 全等情形,我们可以构建一条线段的中点(midpoint): 平分这条线段的点。 2.6 线段AB的中点。 |

|
|
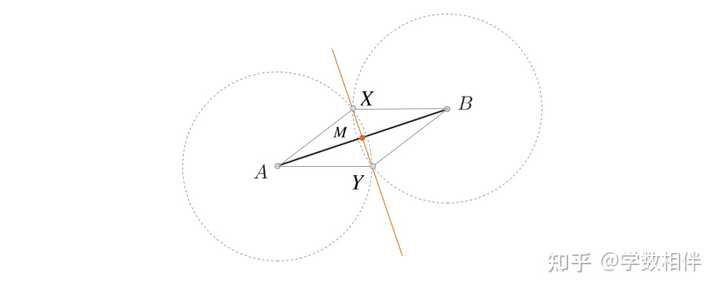
取一个长度 \frac{1}{2}\overline{AB}">r > \frac{1}{2}\overline{AB} , 分别以端点 A,B , 半径为 r 绘制两个圆弧,交于两点 X,Y 。连接 XY 与直线 AB 交于一点 M , 则该点即为线段 AB 的中点。 为什么会这样?我们可以自行分析一下,先应用一次 SSS ,然后再应用一次 SAS 即可。 |
|
|
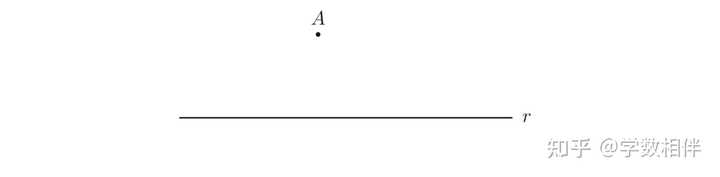
2.7 做过点的直线的垂线 下面例子展示了如何使用三角形全等情形来构造过直线外一点并垂直于该直线的垂线。 给定平面中的线r和s,我们说r垂直于s,s垂直于r,或者简单地说,如果r和s有一个共同点,并且在这个点上形成90°的角度,则r和s是垂直的(在这方面,另见第12页的问题6)。我们将写r⊥s来表示r和s是垂直的。下一个例子展示了如何使用之前研究的同余情况来构造垂直于另一条给定直线并穿过给定点的直线。 例2.11: 给定一条直线 r 和一点 A (可以在直线上),绘制一条过点 A 的 r 的垂线。 情况a) A\not\in r: |
|
|
用圆规其中一脚固定到 A 点,然后调整夹角,绘制半径为 r 的圆,交直线 r 于两点 B,C 。构建线段 BC 的中点 M , 设 s =\overleftrightarrow{AM} 。 则直线 s 即为所求垂线。可以通过 SSS 全等情形来验证。 情况b) A\in r: |

|
|
以 A 为圆心,绘制一个圆交直线 r 于点 B,C 。然后分别以 B, C 为圆心绘制半径为 \frac{1}{2}\overline{BC}">R > \frac{1}{2}\overline{BC} 的两个圆,取这两个圆的两个交点之一 A^\prime , 则直线 \overleftrightarrow{AA^\prime}\perp r 即为所求。 同样可以通过 SSS 来验证。 2.8 绘制平行线(1) |
|
|
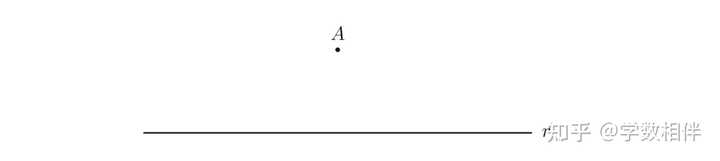
例2.16: 通过点 A 绘制一条直线 s 平行于给定直线 r ,其中 A\not\in r 。 取 r 直线上两个点 C,X ,并连接 AC 。构建角 \angle CAY 使得 \widehat{CAY} = \widehat{ACX} , 其中 X,Y 是关于直线 \overleftrightarrow{AC} 相反的半平面内的。设 s=\overleftrightarrow{AY} 就平行于直线 r 。 |
|
|
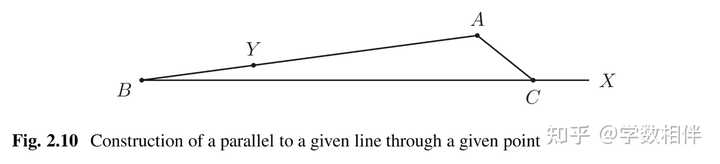
证明上述操作是正确的,我们可以使用反证法,假设 AY, r 相交于一点 B 。 那么我们考虑 C\in BX 的情形( B\in CX, X\in BC 的情形类似)。 通过构造过程,我们知道 \widehat{BAC} = \widehat{YAC}= \widehat{ACX} 。 另外,因为 \angle ACX 是三角形 ABC 的一个外角,因此就有 r 和直线外一点 A\not\in r , 使用尺规作图绘制过点 A 且平行于 r 的直线。 |
|
|
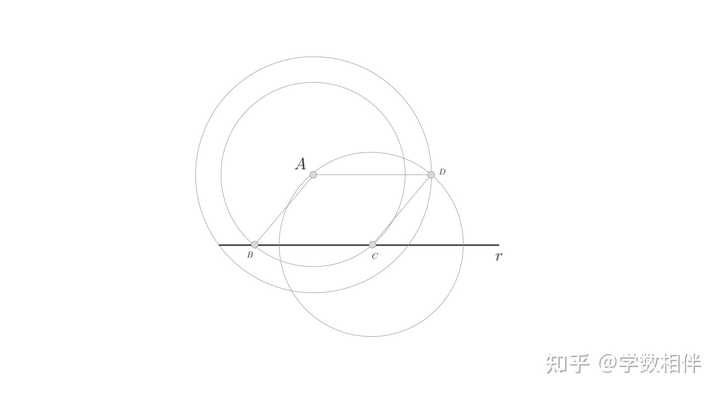
过点 A 绘制一个圆, 半径为 R ,交直线 r 于两个不同的点 B, C 。过点 A 绘制一个圆,半径为 \overline{BC} 。过点 C 绘制一个圆,半径为 R ,也就是跟步骤1中的圆半径一样。\odot C, \odot B 交于两个点,我们取在 r 同侧的那个交点记作 D 。那么凸四边形 ABCD 为平行四边形, AD\parallel BC , 即为所求。 我们这里的原理是利用两组对边相等的四边形为平行四边形来保证过程的正确性的。 2.10 绘制平行四边形 例2.33: 给定两条边和锐角夹角,绘制平行四边形。 |
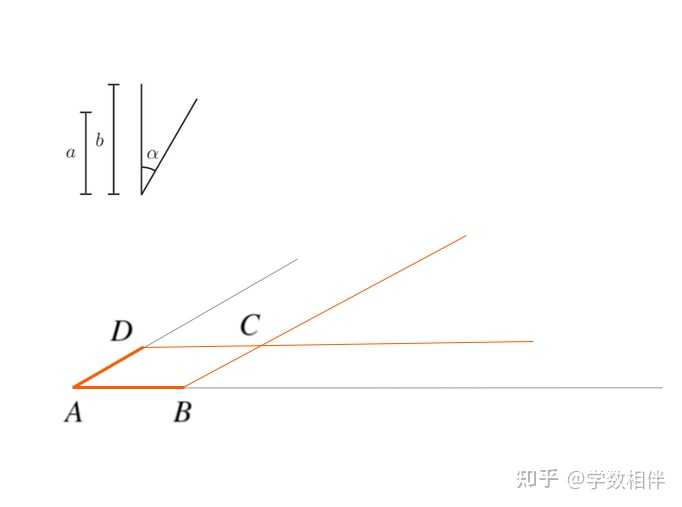
|
|
绘制一条直线 r ,在其上取长度为 b 的线段 AB (也可以选择长度为 a , 注意后面对应即可)。构建一个角度为 \alpha 的角 \angle BAX 。然后在射线 \overrightarrow{AX} 上取线段 \overline{AD} = a ,截点为 D 。然后过点 D 绘制平行于 \overleftrightarrow{AB} 的直线,过点 B 绘制平行于 \overleftrightarrow{AD} 的直线,取它们的交点 C 。则四边形 ABCD 即为所求。2.11 角角边绘制三角形 例题2.34: 给定两个角和一条边,绘制三角形。 |

|
|
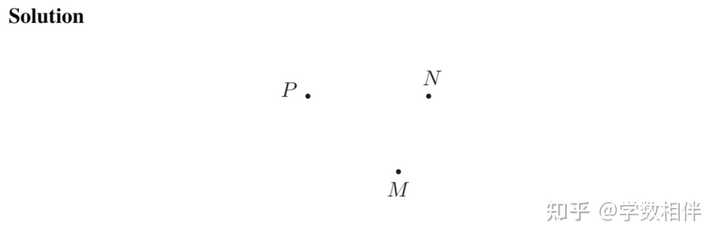
2.12 三边中点绘制三角形 例2.37: 中位线定理应用, 给定三角形的三边中点位置,绘制这个三角形。 |
|
|
|

|
|
2.13 绘制梯形 例2.39: 绘制梯形 |

|
|
2.14 绘制距离给定距离的平行线 |

|
|
2.15 绘制直角三角形 例2.45: 绘制直角三角形 |

|
|
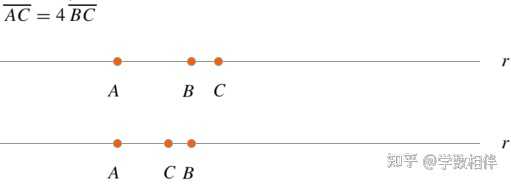
15. 练习1. 练习1.1 1) 直线 l 上四个不同的点 A,B,C,D , l 上存在多少条以这几个点为端点的射线? 答: 一个点可以确定两条射线,因此四个点确定8条射线。 2) 点 A,B,C 位于(situated on a line) r , 其中 C\in AB , 若 \overline{AB} = 10 , \overline{AC} = 4\overline{BC} , 计算 \overline{AC} 。 |
|
|
两种情形,如图所示。因为 C 在线段 AB 上,因此对应下面情形, \overline{AC} = 8 。 3) 设 A,B,C,D 是直线 r 上的四个不同的点,其中 D\in \stackrel{\rightarrow}{AC}, B\in \stackrel{\rightarrow}{DC}, \overline{AC} = \overline{BD} , 证明 \overline{AB} = \overline{CD} 。 |

|
|
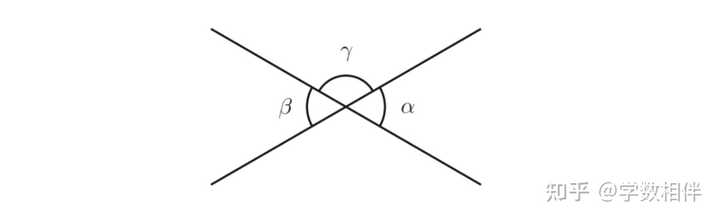
4) 直线 r 上三个点 A,B,C 给定,其中 B\in AC , \overline{AB} = 3, \overline{AC} = 5.5 。使用圆规在线段 AB 上找到一点 D 使得 \overline{AD} =\overline{BC} 。 5) 尺规作图,在平面上标记点 A,B,C ,使 \overline{AB}=5\mathrm{cm}, \overline{AC}=6\mathrm{cm},\overline{BC}=4\mathrm{cm} 。 2. 练习1.2 1) 两个凸区域点交集非空,证明交集也是凸区域。 2) 若角度量加其补角的三倍得到 210^\circ , 求该角的度量? 3) 计算两个互补角的度量,已知其中一个角的两倍等于另一个角度量的三分之一。 4) 若 \alpha,\beta 的对顶角分别为 (9x-2)^\circ, (4x+8)^\circ , 求 \alpha + \beta 的度数表达式。 5) 若锐角比其补角多 76^\circ , 求该锐角度数。 6) 若两直线相交,证明它们所形成的一个角度数为 90^\circ 当且仅当四个角度数都是 90^\circ 。 7) 如下图所示, \begin{aligned}\alpha = \frac{1}{6}(\gamma+\beta)\end{aligned} , 求 \alpha 。 |
|
|
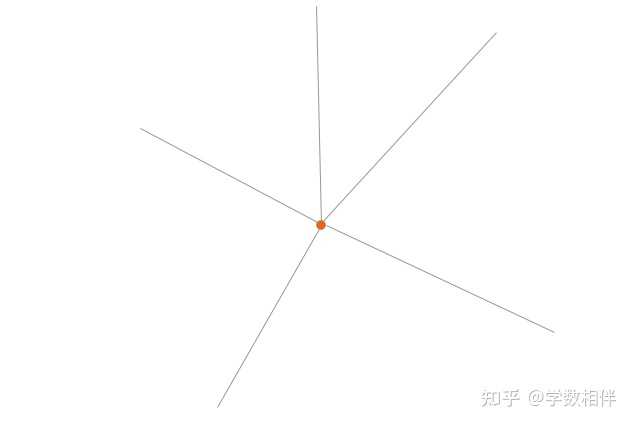
8) 从原点 O 出发的五条射线将平面划分为五个角,它们度数分别与 2,3,4,5,6 成比例,求最大角的度数。 |
|
|
9) 尺规作图,绘制一个角度数为下面两个角度数的和。 |

|
|
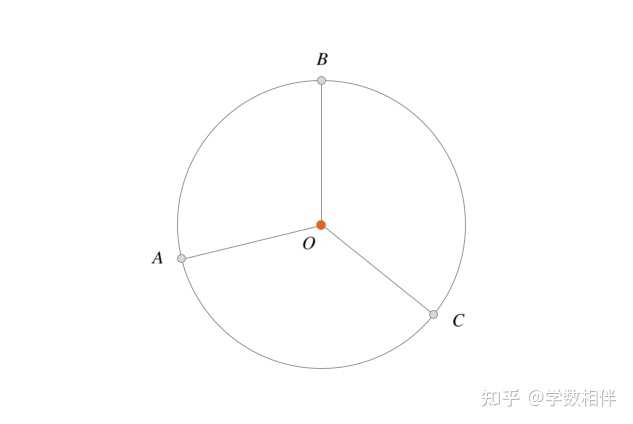
10) 圆 \odot O 上取三个点 A,B,C , 使得 \overset{\LARGE{\frown}}{AB} = \overset{\LARGE{\frown}}{BC} = \overset{\LARGE{\frown}}{AC} , 计算 \angle AOB, \angle BOC, \angle AOC 的度数。 |
|
|
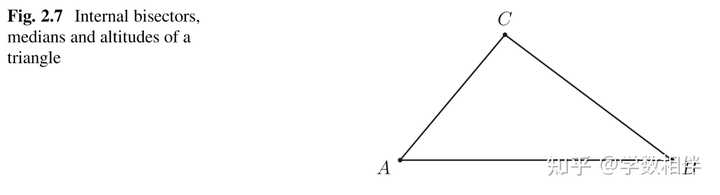
11) 同一个原点 O 的三条射线将平面分成三个角。证明这三个角中至少有一个角度数大于等于 120^\circ , 至少有一个角度数小于等于120^\circ 。 3. 练习1.3 1) 用数学归纳法证明凸多边形对角线数量公式 \begin{aligned}\frac{k(k-3)}{2}\end{aligned} 。 思路说明: 将凸 n+1 边形一条对角线连起来,得到一个三角形与一个 n 边形。 设 A_1A_2\cdots A_kA_{k+1} 为凸 k+1 边形,对角线 A_1A_k 将其分为两个凸多边形: \Delta A_1A_kA_{k+1} 和 k 边形 A_1A_2\cdots A_k 。 A_1A_2\cdots A_kA_{k+1} 多边形的对角线位于三种类型的集合中: A_1A_k 。A_1A_2\cdots A_k 的对角线。A_iA_{k+1}(2\leq i \leq k-1) 。 这三类对角线的数量相加即得到所求的对角线数量 \begin{aligned}\frac{k(k-3)}{2}\end{aligned} 。 2) 凸多边形从其每个顶点可以画凸六边形(hexagon)对角线数量的对角线。那么这个多边形有多少条边? 首先正六边形有9条对角线,而每个凸 n 多边形的每个顶点可以画 n-3 条对角线,因此这个多边形为凸12边形。 3) 三个凸多边形边数等于连续三个自然数。若已知这三个多边形对角线的数量之和为133,计算出最大边数的多边形的边数。 解: 设 n,n+1,n+2 分别表示多边形的边数。使用命题1.12(凸多边形对角线数量公式)得出一个关于 n 的二次方程 \begin{aligned}\frac{n(n-3)}{2} + \frac{(n+1)(n-2)}{2} + \frac{(n+2)(n-1)}{2} = 133\end{aligned}\\整理得 3n^2 - 3n - 270 = 0 \iff n^2 - n - 90 = 0 \implies n = 10 。所以分别是凸10,11,12边形。 4. 练习2.1 a) 举一个例子,表明两个全等三角形,其中一个三角形不可能在平面内刚体运动(移动且不变形)与另一个三角形重合。然而,在空间中刚体运动,则可能达到两个三角形重合。 b) 上面例子中的两个全等三角形在什么意义上彼此不同,以至于这种差异解释了我们不能在平面内刚体运动让它们重合的事实呢? 5. 练习2.2 1) 使用尺规作图,绘制三角形的内角平分线、中线、高线。 |
|
|
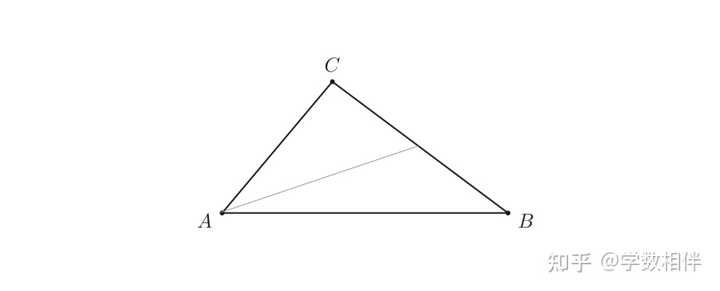
注解: 三角形内角平分线和中线都是位于三角形内部,这点根据它们的定义直接可得。三角形的高线则不一定在三角形内。三角形的三条内角平分线都交于一点,同样的,中线和高线也是如此。这种性质与三角形无关。 2) 设平面内一点 A 和一条直线 r , A\not\in r 。如果 A^\prime 是平面另外一点,满足 \overleftrightarrow{AA^\prime}\perp r , 并且 r 穿过 \overleftrightarrow{AA^\prime} 的中点,那么这个点 A^\prime 和 A 关于直线 r 对称(symmetric), 也称镜像对称。尝试尺规作图找到这样的点 A^\prime 。 3) 尺规作图: 构建三角形 ABC , 已知 \overline{AB} = c, \overline{BC}=a 和关于点 A 的中线长度 m_a 。 |
|
|
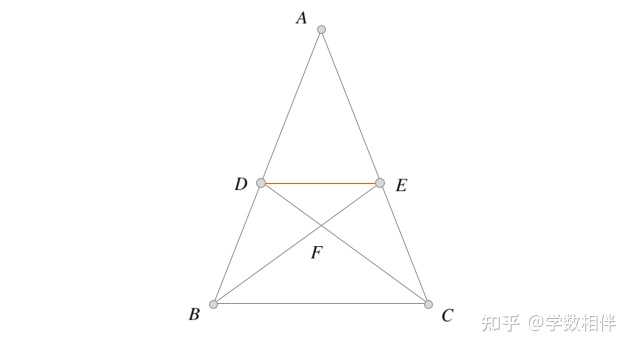
4) 尺规作图: 给定 \overline{AB} = c, \overline{BC} = a, m_a (关于顶点 A 的中线)长度,绘制三角形 \Delta ABC 。 5) 尺规作图: 给定 \overline{AB} =c, \beta_a, \angle BAC = \alpha , 其中 \beta_a 为 A 顶点的角平分线。 6) 设 \Delta ABC 为底边为 BC 的等腰三角形。证明底边三线合一。 7) 设 \Delta ABC, P,M,H 分别为相对于 A 点的内角平分线、中线和高线的足。若 P,M,H 三点重合,证明 \Delta ABC 为底边 BC 的等腰三角形。 8) 设 \Gamma(O,R) 为圆, AB 为其一条弦。若 M\in AB , 证明 \overleftrightarrow{OM}\perp \overleftrightarrow{AB} \iff \overline{AM} = \overline{BM} 。(垂径定理) 6. 练习2.3 1) 直角三角形的 HL 全等情形: 如果两个直角三角形斜边和一条直角边对应相等,则这两个直角三角形全等。 利用勾股定理,三边都相等,因此由 SSS 可证得。 2) \Delta ABC 为底边为 BC 的等腰三角形, D\in AB, E\in AC , \overleftrightarrow{DE}\parallel\overleftrightarrow{BC} , CD, BE 交点为 F ,求证 \overline{BF}=\overline{CF} 。 证明: \Delta ADC\cong \Delta AEB\implies \overline{AD} = \overline{AE}, \widehat{ABE}=\widehat{ACD},\overline{BE}=\overline{CD} 。 然后再证 \Delta DFB\cong \Delta EFC 即可得证结论。 |
|
|
3) \Delta ABC 为底边为 BC 的等腰三角形, 证明相对于边 AB,AC 的高线、中线、内角平分线分别都是相等的。 4) ) \Delta ABC,\widehat{A} = 90^\circ 。设 P\in AC 是 B 点内角平分线的足。已知 \overline{PD}=2 ( P 到 BC 的距离),求 \overline{AP} 。 说明: \Delta BAP\cong \Delta BDP\implies \overline{AP} = \overline{DP}=2 。 |
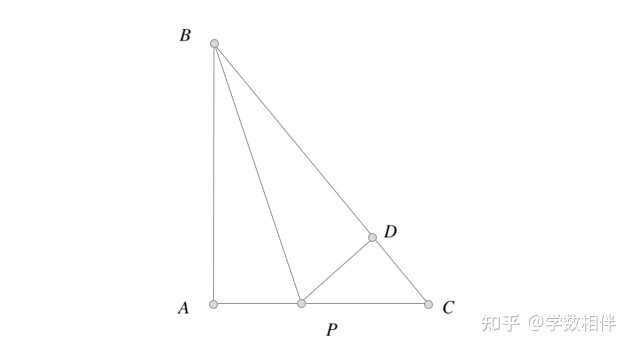
|
|
5) 如下图所示, 已知 \overleftrightarrow{AB}\parallel \overleftrightarrow{CD}, \widehat{ABC} = 3x-20^\circ, \widehat{BCD} = x+40^\circ 。求 x 的值。 |
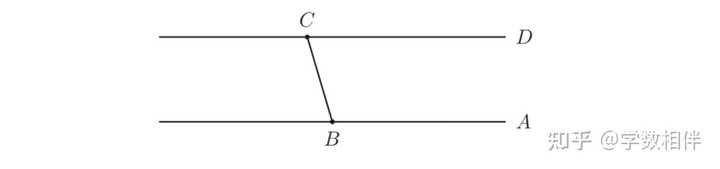
|
|
6) 如下图所示,同位角(corresponding angles): r\parallel s\iff \alpha = \beta 。 |
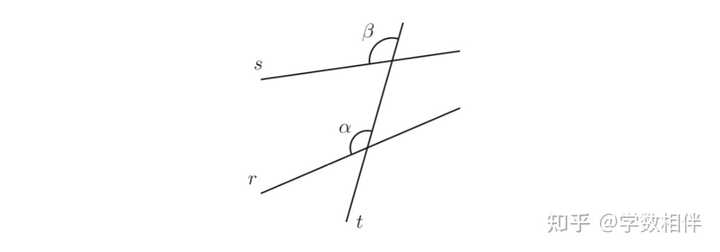
|
|
7) 如下图所示, 若 r\parallel s ,证明 \alpha+\beta = \gamma 。 |
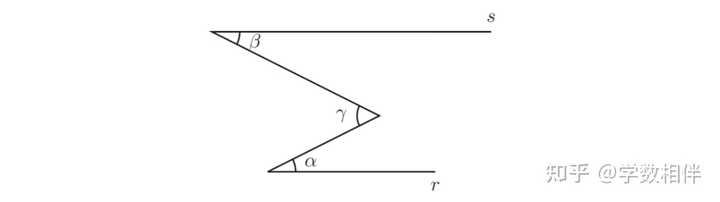
|
|
8) 如下图所示,已知 \widehat{ABC} = 20^\circ, \widehat{BCD} = 60^\circ, \widehat{DEF} = 25^\circ , 若 \overleftrightarrow{AB}\parallel \overleftrightarrow{EF} , 求 \angle CDE 的度数。 |
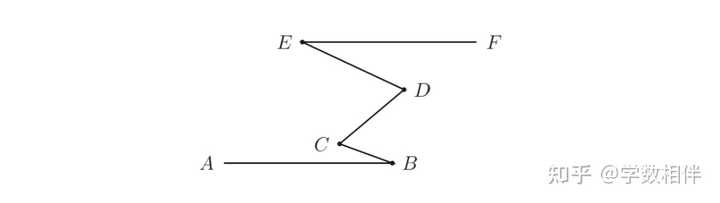
|
|
9) 如下图所示, 证明 \alpha = \widehat{DAB} + \widehat{ABC} + \widehat{BCD} 。 |
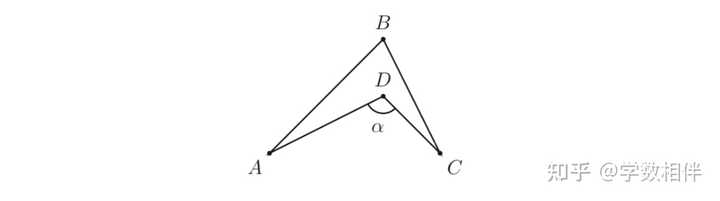
|
|
10) 如下图所示,计算五角星的五个顶点 A,B,C,D,E 所对应角度数之和。 |
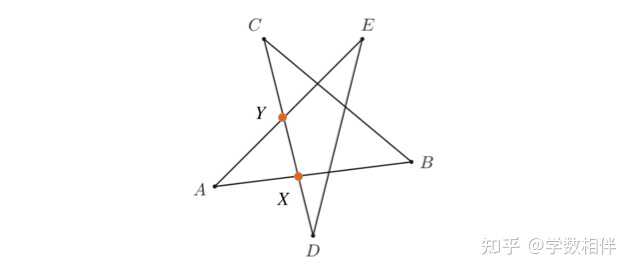
|
|
解: 取 X = AB\bigcap CD, Y = AE\bigcap CD , 则 \Delta AXY 中 \angle AXY, \angle AYX 分别是 \Delta XBC 的 X 点、 \Delta YED 的 Y 点对应的外角。根据外角定理,我们知道 \widehat{A} + \widehat{B}+\widehat{C}+ \widehat{D}+ \widehat{E} = 180^\circ 。 11) 给定凸 n 边形,完成下面的项: (a) 证明交于顶点的 n-3 个对角线将这个多边形划分为 n-2 个三角形。 (b) 证明多边形内角和为 180^\circ(n-2) 。 (c) 证明多边形外角和为 360^\circ (一个顶点只算一个角)。 |
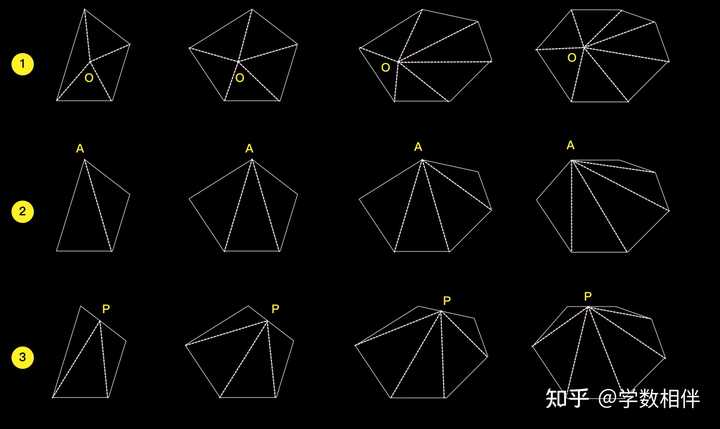
|
|
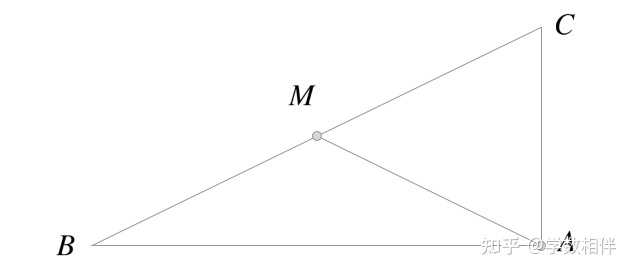
证明思路如上图所示,三种方式。 12) \Delta ABC: \overline{BM} = \overline{MC}=\overline{AM} , 求证 \widehat{BAC} = 90^\circ 。 |
|
|
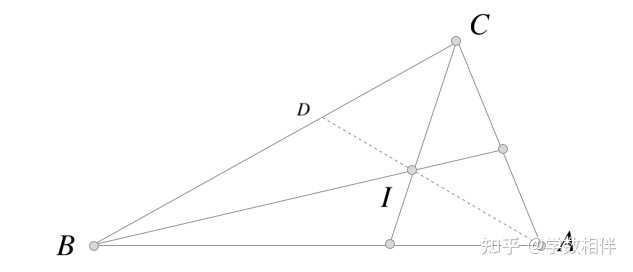
13) 设 \Delta ABC 的内角平分线交点为 I , 求证 \begin{aligned}\widehat{BIC} = 90^\circ + \frac{1}{2}\widehat{BAC}\end{aligned} 。 |
|
|
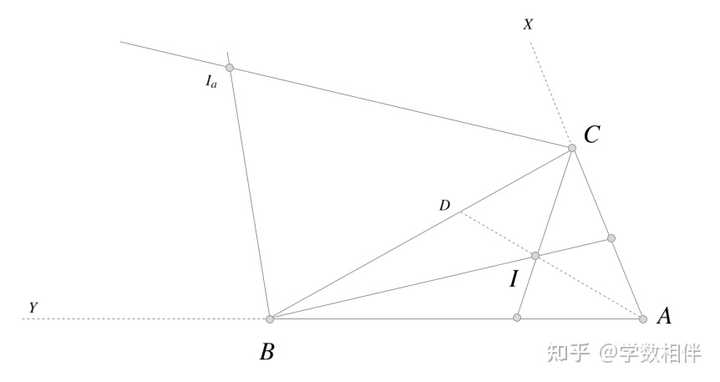
说明: 连接 AI 并延长交 BC 于 D 点。然后 \widehat{BIC} = \widehat{BID} + \widehat{CID} , 则由外角定理得到 \widehat{DIC}= \frac{1}{2}\widehat{ACB} + \widehat{CAB}, \widehat{DIB}= \frac{1}{2}\widehat{ABC} + \widehat{CAB}\\ 整理即得证。 14) \Delta ABC , I 为内心,即三条内角平分线的交点。若 \begin{aligned}\widehat{A} = \frac{1}{8} \widehat{BIC}\end{aligned} , 求 \widehat{A} 。参考上题结论和图。 15) \Delta ABC , I_a 为旁心(excenter相对于顶点 B,C 的外角平分线交点), 求证 \begin{aligned}\widehat{BI_aC} = 90^\circ - \frac{1}{2}\widehat{BAC}\end{aligned} |
|
|
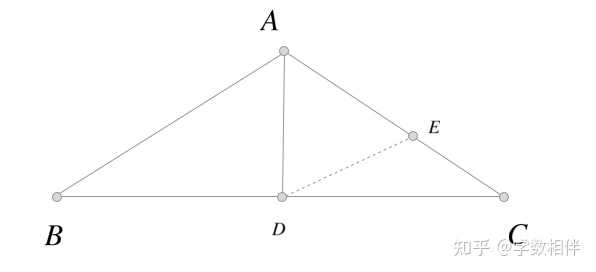
证明: \begin{aligned}\widehat{BI_aC} + \widehat{I_aCB} + \widehat{I_aBC} = 180^\circ \end{aligned} 由外角定理得 \widehat{XCB} = \widehat{CAB} + \widehat{CBA}, \widehat{YBC} = \widehat{BCA} + \widehat{CAB} 。 另外 \Delta ABC: \widehat{CAB} + \widehat{CBA}+\widehat{BCA} = 180^\circ 再加上外角平分线我们可以证得结论(过程略)。 16) \Delta ABC 为底边为 BC 的等腰三角形, D\in BC, E\in AC , 若 \overline{AD} = \overline{AE},\widehat{BAD} = 48^\circ , 求 \widehat{CDE} 。 |
|
|
17) 给定一条直线 r 和一个点 A , 证明仅存在唯一的直线 s: s\perp r, A\in s 。 |

|
|
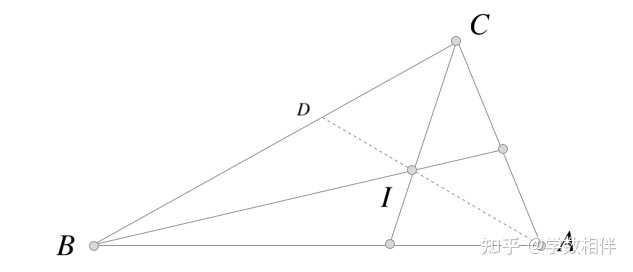
证明: 需要考虑 A\in r, A\not\in r 两种情况。不管哪种情况我们都可以通过反证法来证明。 考虑 A\in r , 存在两条直线 s,t, A\in s,t: s\perp r, t\perp r 。考虑取 B\in s,C\in t , 则 \Delta ABC 内角和大于 180^\circ ,矛盾。 对于 A\not\in r 的情形也是类似。 18) \Delta ABC , I 为内心,即三条内角平分线的交点。 AI 延长交 BC 于 D 。求证 \widehat{ADC} - \widehat{ADB} = \widehat{B} - \widehat{C} 。 |
|
|
证明: 利用外角定理+内角平分线可以直接证明。 19) \Delta ABC 为底边 BC 的等腰三角形, D,F\in AB, E\in AC 是选定的一些点使得 \overline{BC} = \overline{CD} = \overline{DE} = \overline{EF} = \overline{FA} 。计算 \angle BAC 的度量。 |
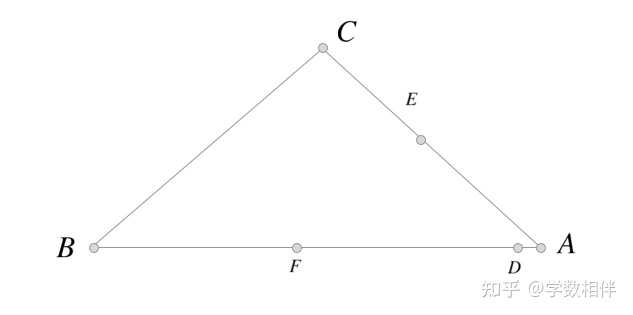
|
|
说明: D, A 重合, \overleftrightarrow{EF}\parallel \overleftrightarrow{BC} , 如果满足 \overline{DE} = \overline{EF} = \overline{FA} 则只能为等边三角形。 20) (TT) ABCDEF 是凸六边形,它的对角线 AD,BE,CF 交于一点 M 。如果 M 是这三条对角线的中点,证明 \widehat{A} + \widehat{B} + \widehat{C} = 360^\circ 。(原书结论有误 180^\circ ) |
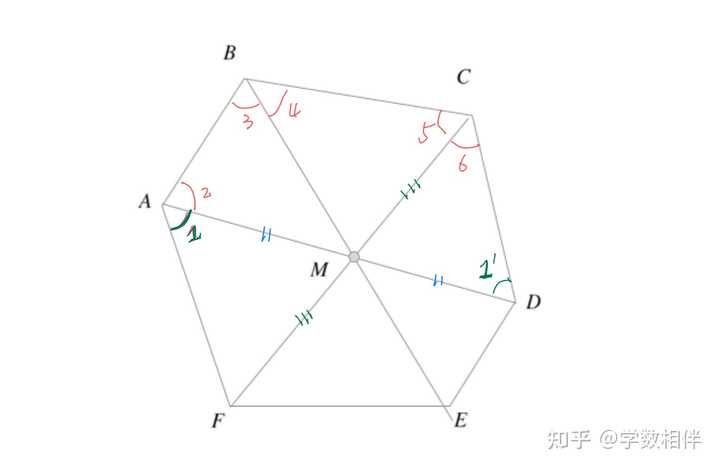
|
|
说明: 所求 \angle A + \angle B + \angle C = \angle 1 + \angle 2 + \angle 3 + \angle 4+ \angle 5+ \angle 6 而 M 为三条对角线的中点,我们可以证得 \Delta AMF\cong \Delta DMC\implies \angle 1 = \angle 1^\prime 。 \angle A + \angle B + \angle C = \angle 1^\prime + \angle 2 + \angle 3 + \angle 4+ \angle 5+ \angle 6 , 刚好是四边形 ABCD 的内角和。 21) \Delta ABC 为底边 BC 的等腰三角形。两个腰上的高都是10, 那么计算下面两种情况: (a) 若 P\in BC , 计算 P 到两个腰 AB, AC 的距离之和。 (b) 若 Q\in \overleftrightarrow{BC}\backslash BC , 计算 Q 到两个腰AB, AC 的距离之差的绝对值。 |
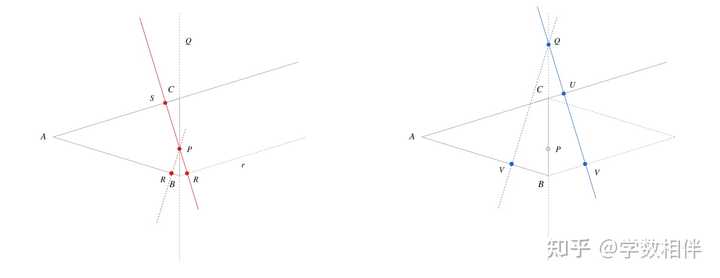
|
|
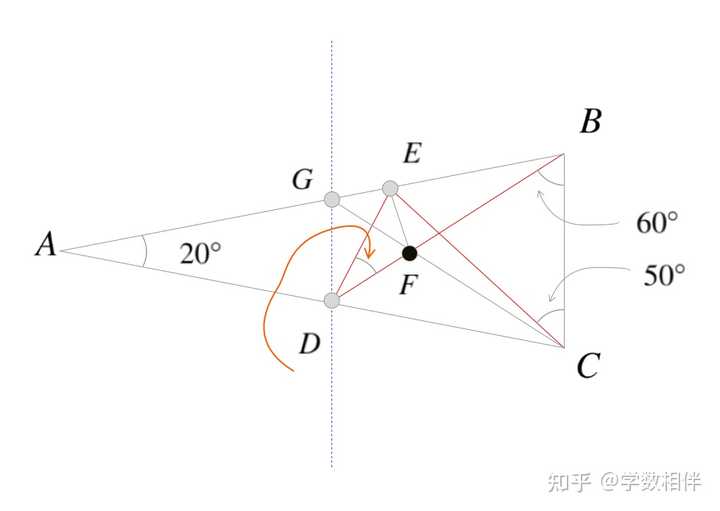
解: 如上图所示,两个答案都是10。可证明 \Delta PRB\cong \Delta PR^\prime B, \Delta QBV\cong \Delta QBV^\prime 。 左图所求实际等于 \overline{RC} , 右图所求实际为 \overline{UV} , 均为腰的高长度。 22) (Soviet Union苏联) 三角形 \Delta ABC 是底边为 BC 的等腰三角形,其中 \widehat{BAC} = 20^\circ 。 D\in AC, E\in AB: \widehat{DBC} = 60^\circ, \widehat{ECB} = 50^\circ , 计算 \widehat{BDE} 。 |
|
|
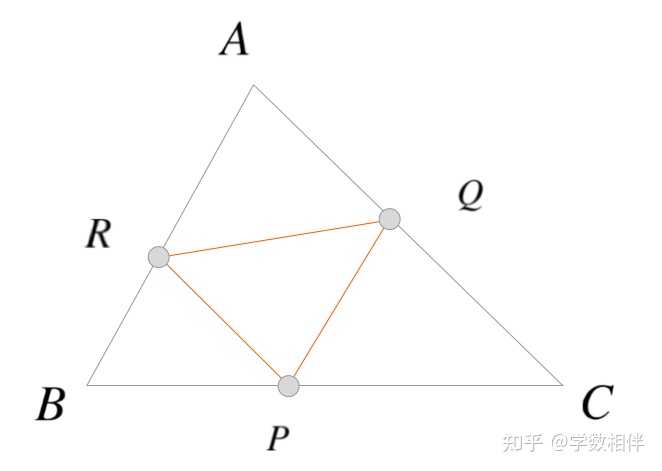
解: 过 D 作 BC 的平行线,交 AB 于 G 。设 CG,BD 交点为 F 。 因为等腰三角形 \Delta ABC , 我们前面证明过 \overline{FB}=\overline{FC}\implies \Delta FBC 为等边三角形 \overline{BC} = \overline{BF} = \overline{FC} 。 我们根据已知角度信息,可以得到 \widehat{GCD} = 20^\circ, \widehat{BGF} = \widehat{BAC} + \widehat{GCA} = 40^\circ 。 另外可计算得到 \widehat{BEC} = 180^\circ - 80^\circ - 50^\circ = 50^\circ \implies \overline{BE} = \overline{BC} 。 于是 \Delta EBF: \overline{BE}=\overline{BF} \implies \widehat{BEF} = \widehat{BFE} =80^\circ 。 \widehat{GEF} = 100^\circ\implies \widehat{EFG} = 180^\circ - 40^\circ - 100^\circ = 40^\circ\implies \overline{GE} = \overline{EF} 。 \overline{DG} = \overline{DF}, \overline{GE} = \overline{EF}, \overline{DE} = \overline{DE}\implies \Delta GED\cong \Delta FED\implies \widehat{GDE} = \widehat{FDE} = 30^\circ 。 7. 练习2.4 1) 等腰三角形的两条边长分别为 38\mathrm{cm}, 14\mathrm{cm} , 求周长。 注意: 该题隐含了腰不能为14。 2) 已知 x\in\mathbb{R}, x+10, 2x+4, 20-2x 为某三角形的三边,确定 x 的范围。 3) 已知 \Delta ABC: \widehat{C} < \widehat{A} < \widehat{B}, \overline{AC} = 27cm, \overline{BC} = 16cm, AB 边长为整数,求其长度的可能值。 4) 已知 \Delta ABC, P\in BC, Q\in AC, R\in AB , 求证 \Delta PQR 周长小于 \Delta ABC 周长。 |
|
|
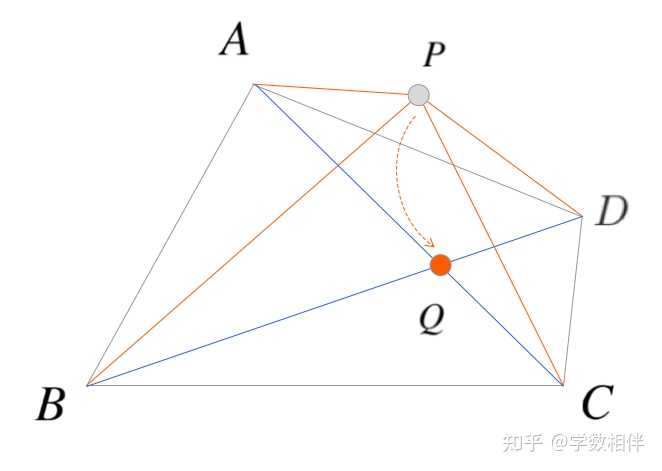
5) 若 a,b,c 为某三角形的三边长,求证 a,b,c 为某三角形的三边长,证明 c^3">a^3 + b^3 + 3abc > c^3 。 c(a^2-ab+b^2) = c[(a+b)^2 - 3ab] \\&> c(c^2 - 3ab) \end{aligned}\\">\begin{aligned} a^3 + b^3 &= (a+b)(a^2 - ab + b^2) \\&> c(a^2-ab+b^2) = c[(a+b)^2 - 3ab] \\&> c(c^2 - 3ab) \end{aligned}\\ 7) 给定凸四边形 ABCD , 证明平面内点 P: \overline{PA}+ \overline{PB}+ \overline{PC}+ \overline{PD} ,使得该和最小的点 P 为该图四边形对角线的交点。 |
|
|
对三角形 \Delta PAC, \Delta PBD 应用三角形不等式即可求证。 8) 设 3\leq n\in\mathbb{Z} , 证明所有凸 n 边形,任意一边长度都小于剩下 n-1 条边长度之和。 数学归纳法即可得证。三角形成立,然后假设 n=k 成立,证明 n=k+1 也成立。 9) 设 m,n\geq 3 , \mathcal{P}, \mathcal{Q} 分别为凸 n,m 边形。若 \mathcal{P} 包含在 \mathcal{Q} 的内部,证明 \mathcal{P} 周长小于 \mathcal{Q} 周长。 |
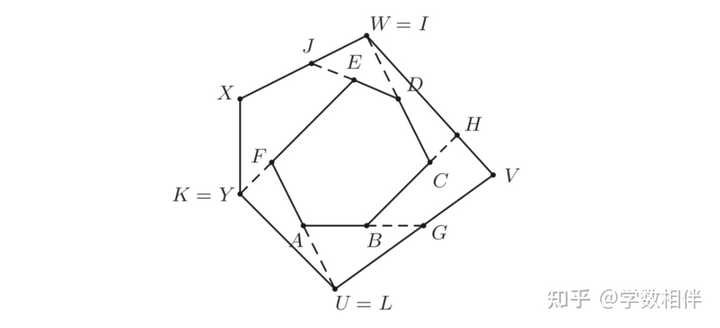
|
|
用上面的图来证明,一般情形类似。 考虑 AUG, BGVH, CHI, DWJ, EJXY, FKL 这些凸多边形。 AUG: \overline{AB} + \overline{BG} < \overline{AU} + \overline{UG}\\ BGVH: \overline{BC} + \overline{CH} < \overline{BG} + \overline{GV} + \overline{VH}\\ CHW: \overline{CD} + \overline{WD} < \overline{CH} + \overline{WH}\\ DWJ: \overline{ED} + \overline{EJ} < \overline{WD} + \overline{JW}\\ JEYX: \overline{FE} + \overline{FY} < \overline{XY} + \overline{XJ}+\overline{JE}\\ YFU: \overline{FA} + \overline{AU} < \overline{FY} + \overline{YU}\\ 左右相加即得证。 10) 如下图所示,射线 r\perp s ,尺规作图绘制点 B\in r, C\in s , 使得 \overline{AB}+\overline{BC} + \overline{CD} 尽可能小。 |
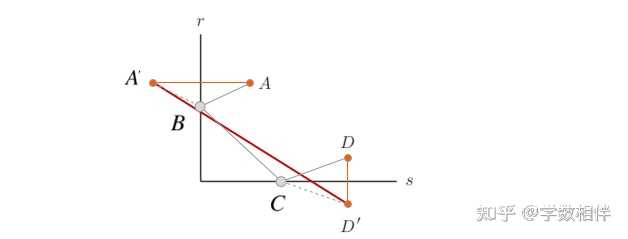
|
|
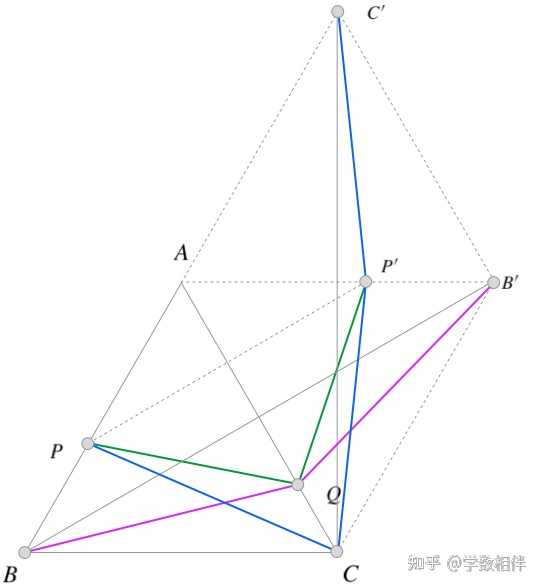
11) 已知等边 \Delta ABC 变长为 l , P\in AB, Q\in AC (非顶点), 求证 2l">\overline{BQ} + \overline{PQ} + \overline{CP} > 2l 。 |
|
|
证明: P,P^\prime 关于 AC 对称, B,B^\prime 关于 AC 对称, C,C^\prime 关于 AB^\prime 对称。把 \overline{BQ} + \overline{PQ} + \overline{CP} 长度转换为 \overline{BQ} + \overline{P^\prime Q} + \overline{C^\prime P^\prime} 问题,然后考虑凸四边形 PQP^\prime C^\prime ,三边之和大于第四边,即得证。 12) 设 \Delta ABC: \overline{AB} \geq \overline{AC}\geq \overline{BC} , 给定三角形内部的一个点 P , 证明 \overline{PA} + \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC} 。 |
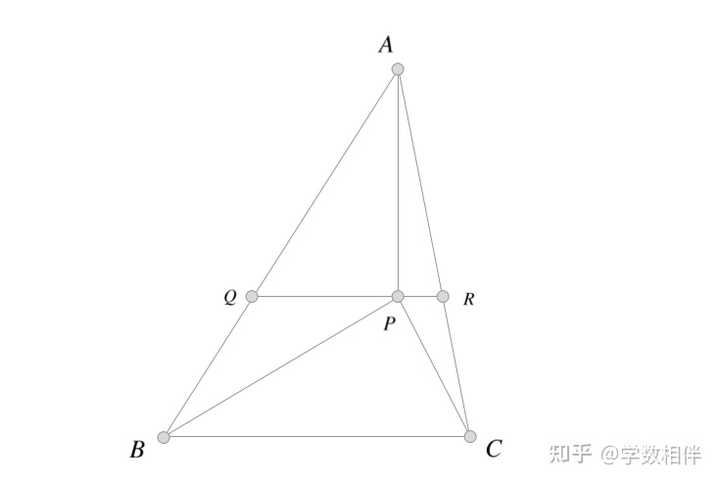
|
|
证明: 过 P 作 BC 的平行线,分别交 AB, AC 于点 Q,R 。不失一般性,考虑 \overline{PB} + \overline{PC} < \overline{BQ} + \overline{QR} + \overline{CR} < \overline{BQ} + \overline{AQ} + \overline{CR} 。于是就得到 \overline{PA} + \overline{PB} + \overline{PC} < \overline{BQ} + \overline{AQ} + \overline{CR} + \overline{AR} = \overline{AB} + \overline{AC}\\ 其他情形类似。 13) (Soviet Union) 某个国家,任意两个城市之间的距离不相等。如果飞机从某城市出发飞往最近的城市,请证明任何一个城市降落的飞机不超过五架。 |
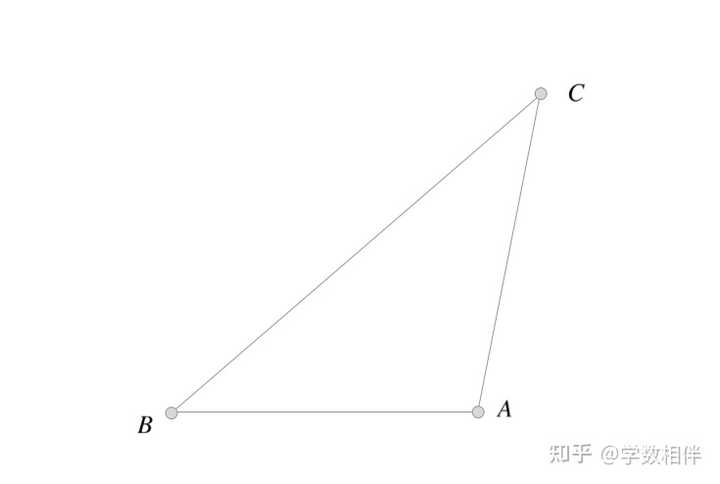
|
|
证明: 若从城市 B,C 出发的飞机都降落到 A 城市,我们根据题意知道 \widehat{BAC} > 60^\circ , 考虑城市 A , 那么降落到 A 城市的飞机数量不能超过6,否则就得到矛盾。圆周角为 360^\circ 。 |

|
|
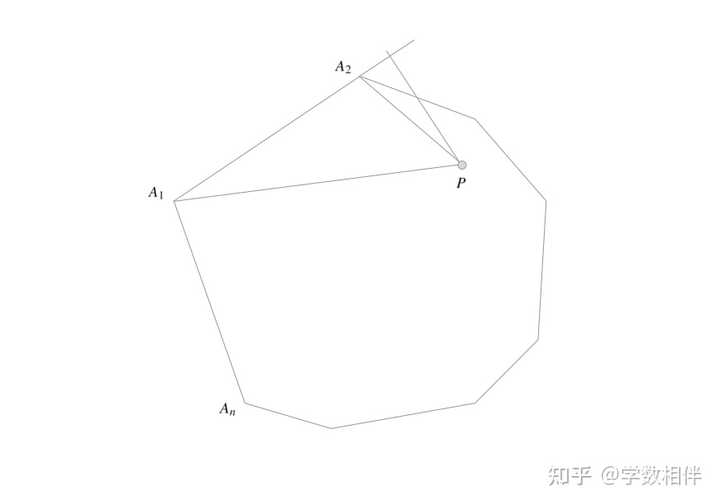
14) 凸多边形 A_1A_2\cdots A_n ,点 P 位于其内部。证明存在 1\leq i\leq n 使得 P 到边 A_iA_{i+1} 的垂足位于线段 A_iA_{i+1} 内( A_{n+1} = A_1 )。 |
|
|
证明: 反证法,假设 P 到 \overleftrightarrow{A_1A_2} 的垂足落在线段 A_1A_2 之外,那么就有 \widehat{PA_1A_2} \geq 90^\circ\lor \widehat{PA_2A_1} \geq 90^\circ 。 不失一般性,不妨设 \widehat{PA_2A_1} \geq 90^\circ , 因为其余的垂足也都落在了多边形边线段之外,那么自然就能得到 \widehat{PA_2A_2} \geq 90^\circ,\cdots, \widehat{PA_nA_{n-1}} \geq 90^\circ, \widehat{PA_1A_n} \geq 90^\circ\\ 于是我们就得到 \overline{PA_2} > \cdots> \overline{PA_n} > \overline{PA_1}\\">\overline{PA_1} > \overline{PA_2} > \cdots> \overline{PA_n} > \overline{PA_1}\\ 显然不可能,所以假设不成立,结论成立。 8. 练习2.5 1) 如果两条线段相等且平行,证明它们的端点刚好是某个平行四边形的顶点。 |
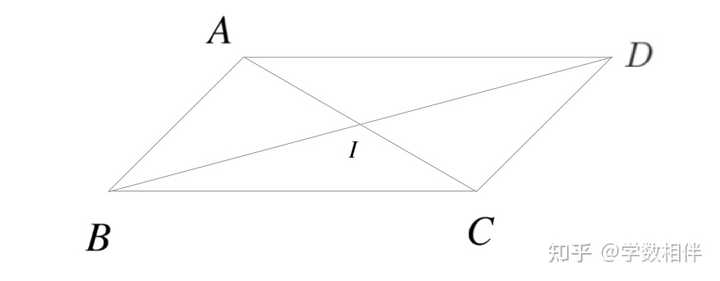
|
|
证明: 设 \overline{AB} \overset{\parallel}{=} \overline{CD} , 设 I \in AC\bigcap BD ,则 \Delta ABI\cong \Delta CDI 。很容易证明结论成立。 2) 证明三角形中线将三角形分成四个全等的三角形。 |
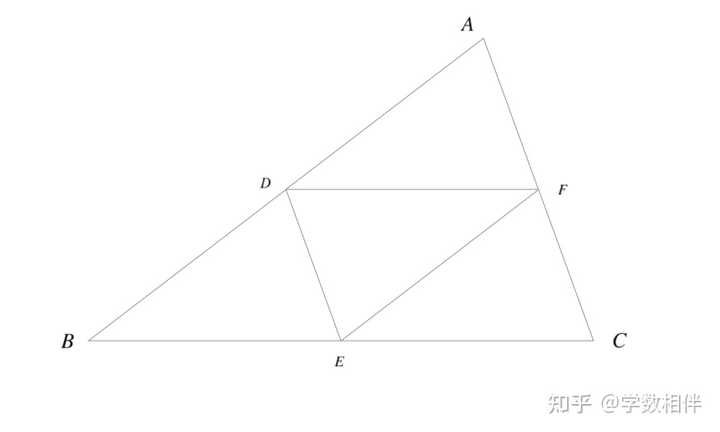
|
|
3) 任意四边形 ABCD 的四条边的中点恰好是某平行四边形的四个顶点。 |
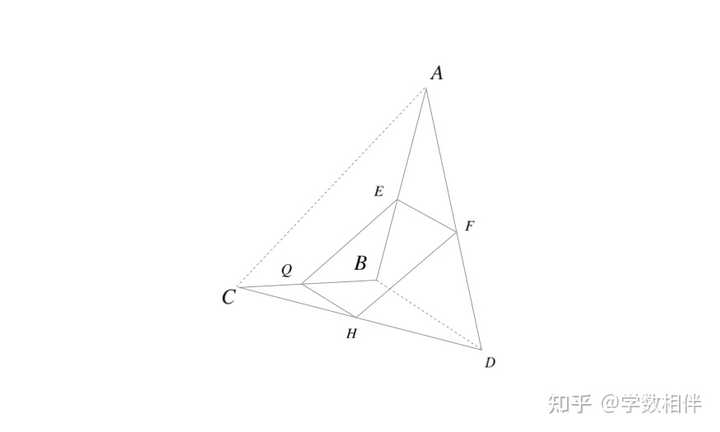
|
|
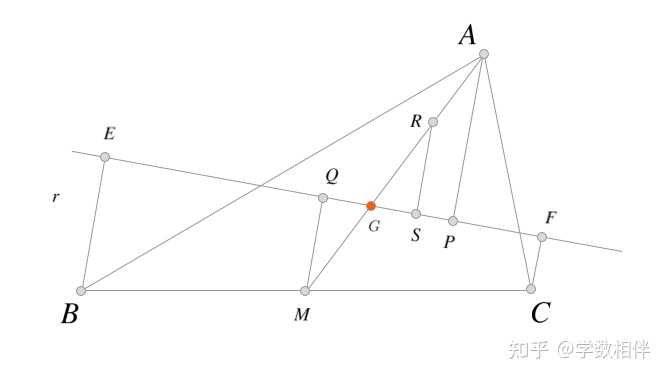
4) 设 \Delta ABC 的重心 G , 设过 G 的直线 r 将顶点 A 和 B,C 分割在直线两侧,求证 A 到 r 的距离等于 B,C 到 r 的距离之和。 |
|
|
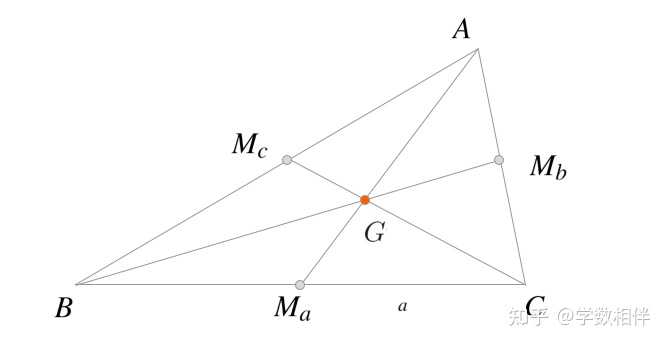
证明: 首先重心 G 为三角形 \Delta ABC 三条边中线的交点。不妨取 BC 的中点 M , AG 的中点 R ,然后分别从 M,R, A 引直线 r 的垂线,设三条垂线在 r 上的垂足分别为 Q,S,P 。 B,C 到直线 r 垂线的垂足为 E,F 。 要证明 \overline{BE} + \overline{CF} = \overline{AP}\iff 2\overline{MQ} = \overline{AP} \iff \overline{MQ} = \overline{RS} ,过程略。 5) 尺规作图: 已知三角形的其中一条边 \overline{BC} = a ,以及边 BC, AC 上的中线长 m_a, m_b ,绘制该三角形。 |
|
|
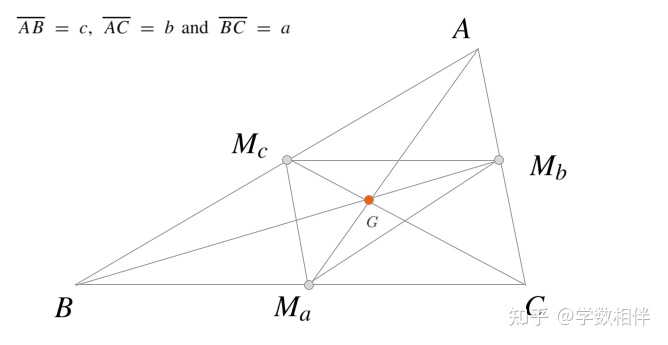
说明: 先构造 \Delta BM_a G , 利用三边长度构造。然后延长 BM_a 为自身两倍得到点 C 。然后延长 M_a G 为自身三倍得到顶点 A 。\Delta ABC 即为所求。 6) 证明任意三角形中, 中线之和小于等于 3p , 大于等于 3p/2 ,其中 p 为半周长。 |
|
|
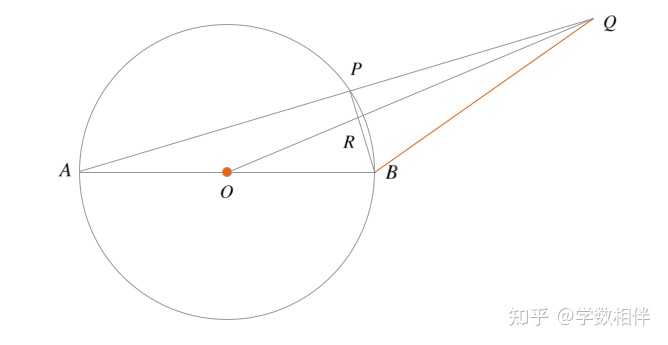
证明: c\\ \Delta AGC: \frac{2}{3}(m_a+m_c) > b\\ \Delta AGC: \frac{2}{3}(m_b+m_c) > a \end{array} \right\} \implies m_a+m_b+m_c > \frac{4}{3}(a+b+c) = \frac{2}{3}p \end{aligned}\\">\begin{aligned} \left. \begin{array}{ll} \Delta AGB: \frac{2}{3}(m_a+m_b) > c\\ \Delta AGC: \frac{2}{3}(m_a+m_c) > b\\ \Delta AGC: \frac{2}{3}(m_b+m_c) > a \end{array} \right\} \implies m_a+m_b+m_c > \frac{4}{3}(a+b+c) = \frac{2}{3}p \end{aligned}\\\begin{aligned} \left. \begin{array}{ll} \Delta AM_aB: m_a < c + \frac{a}{2}\\ \Delta BM_bC: m_b < a + \frac{b}{2}\\ \Delta CM_cA: m_c < b + \frac{c}{2} \end{array} \right\} \implies m_a+m_b+m_c < \frac{3}{2}(a+b+c) = 3p \end{aligned}\\ 7) (England)圆 \Gamma(O, R) ,直径 AB , 弦 AP 延长至两倍到点 Q ,即 \overline{AP} = \overline{PQ} , 设 OQ\bigcap BP = \{R\} 。求比值 \overline{RQ} /\overline{RO} 。 |
|
|
说明: 这个题目看似很难,其实很简单,只要看清 R 为 \Delta ABQ 的重心即可。因此比值为2。 8) 如下图所示梯形,求两底边中点连线的长度。 |
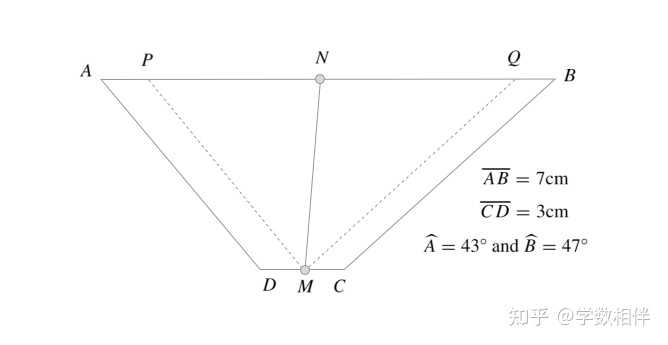
|
|
说明: 过下面底边中点 M 分别作 AD, BC 的平行线,则根据条件可知 \widehat{PMQ} = 90^\circ , 因此所求的 \overline{MN} = \frac{1}{2}\overline{PQ} 。 9) 如下图,直线 r 与平行四边形 ABCD 不相交,其中 A,B,C 到 r 距离分别为 2,3,6 ,求 D 到直线 r 的距离。 |
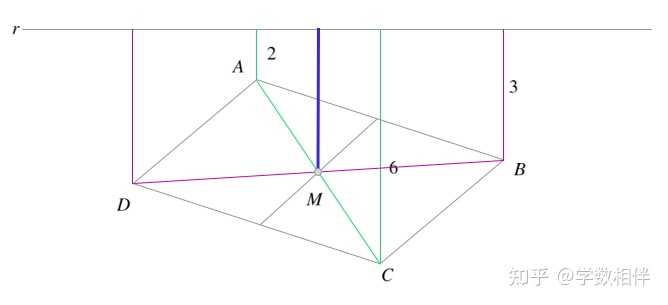
|
|
说明: 如上图所示,对图中粉色和青色梯形分别应用中线定理我们就可以得到答案。 10) |

|
|
送礼物 还没有人送礼物,鼓励一下作者吧 |
|
有。说明空间感不好,以及逻辑思维薄弱。高中回挂掉 |
|
你可能在弧度制就开始崩了 |
|
不参加竞赛没有一点问题,高中考都不考。立体几何一般都是建系算,坐标一标图都可以不要那种。 |
|
肯定有啊,基础要掌握好,点到线,线到面,然后面构成了立体。 |
|
|
| [收藏本文] 【下载本文】 |
| 两性话题 最新文章 |
| 官方通报小洛熙术后离世过程,主刀医师执业 |
| 动物园允许游客与幼狮近距离互动,园方回应 |
| 长得不好看的人吃雌二醇会变漂亮吗? |
| 草莓是农残最高的水果吗? |
| 国家卫健委称自愿紧急救助免责,如何影响人 |
| 研究发现中国人大脑发育约 38 岁达顶峰,峰 |
| 男人一直不那个身体会怎样? |
| 郭继承说每年中国死于腹泻50多万是西方医学 |
| 怎么提升初中数学平面几何大题? |
| 男生裸检会尴尬吗? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |